CAT Quantitative Aptitude Questions | Questions for CAT - Coordinate Geometry

The question is from CAT Coordinate Geometry. This is about area of a segment. We need to find out the area of intersecting region between a circle and a chord. Take Geometry, add one unit of algebra; take a diagram, explain it with x's and y's. For the purists, it is geometry without the romance, for the pragmatists it is Geometry with expanded scope. It is important to cover ideas from Coordinate Geometry in your CAT Preparation.

Question 6: Find the area of the region that comprises all points that satisfy the two conditions x² + y² + 6x + 8y ≤ 0 and 4x ≥ 3y?

1. 25π
2. 25\\frac{π}{4}\\)
3. 25\\frac{π}{2}\\)
4. None of these

Video Explanation

Explanatory Answer

Method of solving this CAT Question from CAT Coordinate Geometry: If a question looks very tough, perhaps there is some special factor that simplifies it. Perhaps a particular chord is actually a diameter?

x² + y² + 6x + 8y < 0
x² + 6x + 9 – 9 + y² + 8y + 16 – 16 < 0
(x + 3)² + (y + 4)² < 25

This represents a circular region with centre (–3, –4) and radius 5 units. Substituting x = y = 0, we also see that the inequation is satisfied. This means that the circle also passes through the origin. To find out the intercepts that the circle cuts off with the axes, substitute x = 0 to find out the y–intercept and y = 0 to find out x–intercept. Thus x–intercept = –6 and y–intercept = –8.



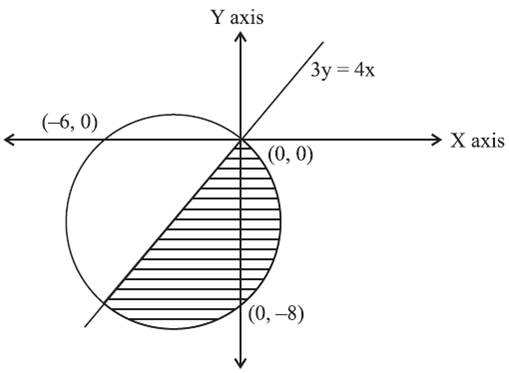
Now, the line 4x = 3y passes through the point (–3, –4). Or this line is the diameter of the circle. The area we are looking for is the area of a semicircle.
Required area = 25\\frac{π}{2}\\)

The question is "Find the area of the region that comprises all points that satisfy the two conditions x² + y² + 6x + 8y ≤ 0 and 4x ≥ 3y?"

Hence, the answer is 25\\frac{π}{2}\\) sq units

Choice C is the correct answer.