Learn from 5 time CAT 100%iler | Best CAT Online Coaching | CAT Preparation

CAT Quantitative Aptitude Questions | Questions for CAT - Coordinate Geometry

CAT Questions | CAT Coordinate Geometry | Points equidistant from lines

× CAT Questions

CAT Quantitative Aptitude
HCF and LCM Factors Remainders Factorials Digits Ratios,Mixtures;Averages Percents; Profits; SICI Speed & Time; Races Logarithms and Exponents Pipes,Cisterns; Work,Time Set Theory Geometry Mensuration Trigonometry Linear & Quadratic Equations Functions Inequalities Polynomials Progressions Permutation Probability
CAT Verbal
Para Jumble Sentence Correction Sentence Elimination Paragraph Completion Reading Comprehension Critical Reasoning Word Usage Para Summary Text Completion
CAT LR DI
DI LR: Bar Graphs DI LR: Pie Charts DI LR: Multiple Graphs DI LR: Word Problems DI LR: Line Graphs DI LR: Sequencing DI LR: Grid Puzzles DI LR: Math Puzzles DI LR: Visualization DI LR: Other Patterns DI LR: CAT 2017 Cet DI LR: CAT 2017 Rural Survey DI LR: CAT 2017 Happiness DI LR: CAT 2017 Airlines DI LR: CAT 2017 Travel Route DI LR: CAT 2017 Food Delivery DI LR: CAT 2017 Square Layout DI LR: CAT 2017 Team Project DI LR: CAT 2017 Assets DI LR: CAT 2017 Pizza DI LR: CAT 2017 Electives DI LR: CAT 2017 Chess DI LR: CAT 2017 Dorms DI LR: CAT 2017 Tea DI LR: CAT 2017 Friends DI LR: CAT 2017 Security Scan

CAT Online Coaching

CAT Questions

The question is from CAT Coordinate Geometry. This is about Points equidistant from lines. We need to find out the equation of a line which can be formed from the points which are equidistant from another given line. Take Geometry, add one unit of algebra; take a diagram, explain it with x's and y's. For the purists, it is geometry without the romance, for the pragmatists it is Geometry with expanded scope. CAT exam does test one on ideas from CAT Coordinate Geometry once in a while. It is important to cover ideas from Coordinate Geometry in your CAT Preparation

Question 4: What is the equation of a set of points equidistant from the lines y = 5 and x = –4?

x + y = –1
x – y = –1
x + y = 1
–x + y = –1

Video Solution

Explanatory Answer

Best CAT Online Coaching
Try upto 40 hours for free
Learn from the best!

2IIM : Best Online CAT Coaching.

Video Explanation

Best CAT Coaching in Chennai

CAT Coaching in Chennai - CAT 2022
Limited Seats Available - Register Now!

Explanatory Answer

Method of solving this CAT Question from CAT Coordinate Geometry : Set of points equidistant from two straightlines must lie on the angle bisector of the line angle formed at the point of intersection. Try proving this. Hint: Use congruence.

Let us try to draw the given lines on the coordinate plane.
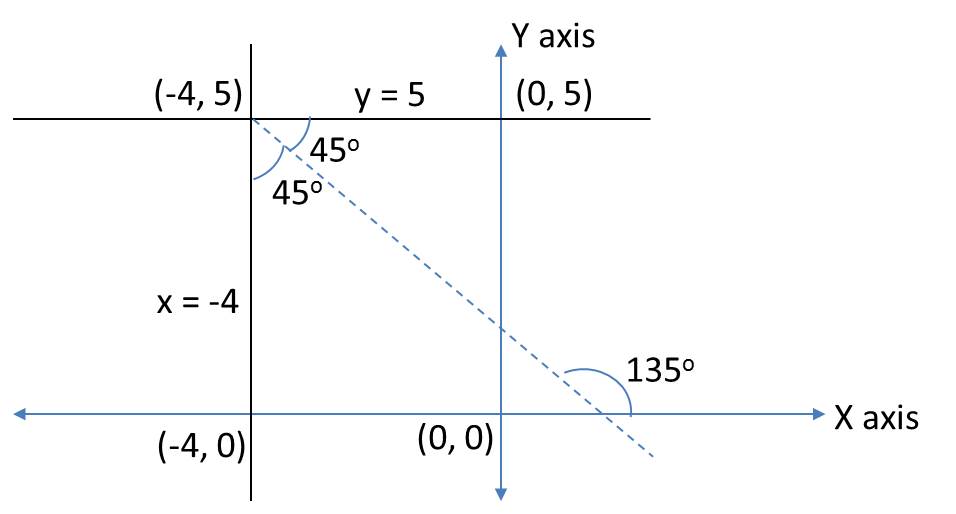
CAT : Geometry: Coordinate Geometry Line

A set of points equidistant from the given two lines should lie on the dotted line as indicated. You can think of it as the perpendicular bisector to the base of an isosceles triangle formed by (–4, 5) and the two points on x = –4 and y = 5.

Or, the set of points equidistant from two lines form the angle bisector of the angle formed at the point of intersection of the two lines. The angle between these two lines is 900. Importantly, the lines are parallel to the axes. So, thinking of the line that is the angle bisector of this angle should not be too difficult.

This dotted line is at an angle of 135^o with respect to the positive direction of x–axis and also passes through (–4, 5).

Slope = m = tan (135^o) = –1.
Therefore, the equation is given by (y – y₁) = m

(x – x₁) where (x₁, y₁) is (–4, 5).
(y – 5) = –(x + 4)
x + y = 1