CAT Quantitative Aptitude Questions | CAT Algebra - Inequalities questions

The question is about maximum possible value. Our task is to maximize the given modulus that is tricky. Inequalities are crucial to understand many topics that are tested in the CAT exam. Having a good foundation in this subject can help us tackle questions in Coordinate Geometry, Functions, and most importantly in Algebra. A range of CAT questions can be asked based on this simple concept.

Question 11: a, b, c are distinct natural numbers less than 25. What is the maximum possible value of |a – b| + |b – c| – |c – a|?

1. 44
2. 46
3. 23
4. 21

Video Explanation

Explanatory Answer

Method of solving this CAT Question from Algebra - Inequalities : Visualising the terms in a number line would be heplful!

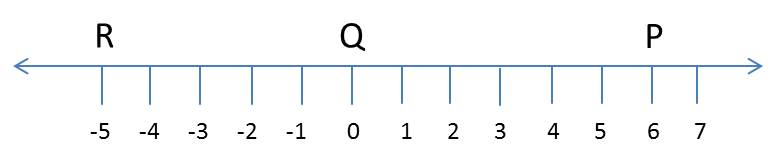
For any two points M, N on the number line representing numbers m, n the distance MN = | m - n|.
So, for three points, P, Q and R on the number line |p – q|, |q – r|, |r – p| are distances between three pairs of points on the number line.

In this case, we are trying to find maximum value of |a – b| + |b – c| – |c – a|. If b lies between a and c, the above value would be zero. So, b should not be between a and c.
The best case scenario would be if a, c were very close to each other and far from b. Let us try b = 24, a = 1, c = 2.
In this case |a – b| + |b – c| – |c – a| = 23 + 22 – 1 = 44. This is the maximum possible value.

We could also have b = 1, a = 24, c = 23,
|a – b| + |b – c| – |c – a| = 23 + 22 – 1 = 44.

The question is "What is the maximum possible value of |a – b| + |b – c| – |c – a|?"

Hence the answer is "44"

Choice A is the correct answer.