CAT Quantitative Aptitude Questions | Geometry Questions for CAT - Trigonometry

The question is from CAT Geometry - Trigonometry. This is about Heights and Distances. We need to find out the height of a broken tree before it was broken. Trigonometry is an important topic for CAT Preparation for the CAT Exam. Trigonometric ideas can be completely opposite, as in, some questions test lot of common sense with direction, heights and distances, while others could test you on identities. CAT exam could test one on both these fronts. Make sure you master both in CAT - Trigonometry.

Question 15: A tall tree AB and a building CD are standing opposite to each other. A portion of the tree breaks off and falls on top of the building making an angle of 30^°. After a while it falls again to the ground in front of the building, 4 m away from foot of the building, making an angle of 45^°. The height of the building is 6 m. Find the total height of the tree in meters before it broke.

1. 27√3 + 39
2. 12√3 + 10
3. 15√3 + 21
4. Insufficient Data

Explanatory Answer

Method of solving this CAT Question from CAT Geometry - Trigonometry : Comparing the broken tree to the opposite building can help!

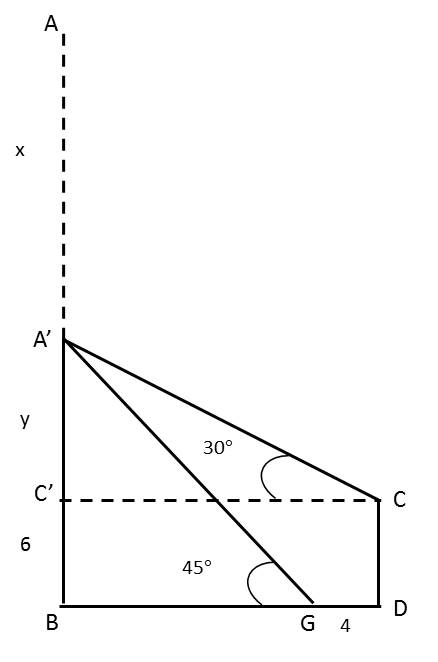
Let the broken portion of tree AA’ be x. Hence A’C = A’G = x

From the figure, total height of the tree = x + y + 6
Consider triangle A’BG, tan 45° = \\frac{A’B}{BG}\\)
1 = \\frac{y + 6}{BG}\\)
Or BG = y + 6

Consider triangle A’C’C, tan 30° = \\frac{A’B}{C’C}\\)
\\frac{1}{√3}\\) = \\frac{y}{BG + 4}\\)
\\frac{1}{√3}\\) = \\frac{y}{y + 6 + 4}\\)
y√3 = y + 10
or y = \\frac{10}{√3 - 1}\\)
= \\frac{10}{√3 - 1}\\) * \\frac{√3 + 1}{√3 + 1}\\)
= \\frac{10(√3 + 1)}{2}\\)
Therefore y = 5(√3 + 1)
Take sin 30° to find x
sin 30° = \\frac{A'C'}{A'C}\\)
\\frac{1}{2}\\) = \\frac{y}{x}\\)
or x = 2y
Height of the tree = x + y = 6
= 2 * 5(√3 + 1) + 5(√3 + 1) + 6
= 10√3 + 10 + 5√3 + 5 + 6
= 15√3 + 21 meters

The question is "To find the total height of the tree in meters before it broke"

Hence, the answer is 15√3 + 21

Choice C is the correct answer.