CAT Questions | CAT LR DI

Solve this DILR Question on Chessboard from CAT 2017. This set is on the easier spectrum of questions that appear in CAT DILR Section. You are expected to answer the questions that follow, based on the simple rules as to how the pieces on a Chessboard move. If you would like to take these questions as a Quiz, head on here to take these questions in a test format, absolutely free.

CAT DILR : 2017 slot 2 questions

Chessboard

In an 8 X 8 chessboard a queen placed anywhere can attack another piece if the piece is present in the same row, or in the same column or in any diagonal position in any possible 4 directions, provided there is no other piece in between in the path from the queen to that piece. The columns are labelled a to h (left to right) and the rows are numbered 1 to 8 (bottom to top). The position of a piece is given by the combination of column and row labels. For example, position c5 means that the piece is in cth column and 5th row.

Question 3: If the other pieces are only at positions al, a3, b4, d7, h7 and h8, then from how many positions the queen cannot attack any of the pieces?

1. 0
2. 3
3. 4
4. 6

Video Explanation

Explanatory Answer

Method of solving this Question on CAT DILR

General Solution

The columns are labelled a to h (left to right) and the rows are numbered 1 to 8 (bottom to top). The position of a piece is given by the combination of column and row labels.



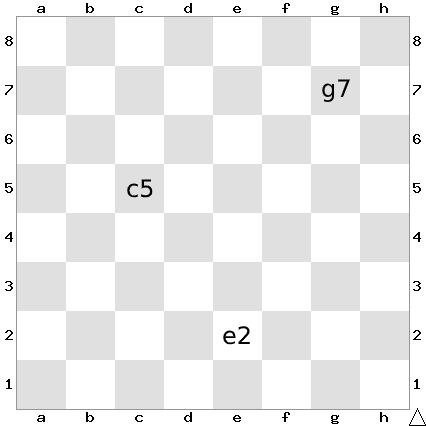
Let us think about the cells that will definitely get covered.
We eliminate 5 rows and 4 columns straight-away



Now, let us go after the diagonals



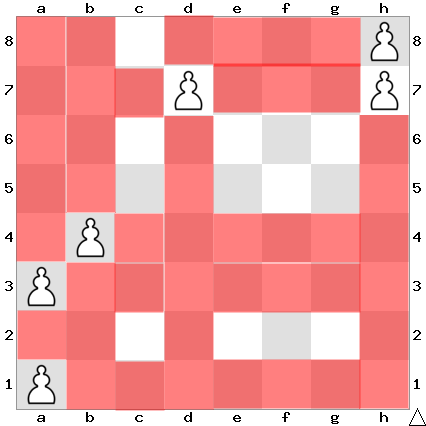
There are 4 cells remaining



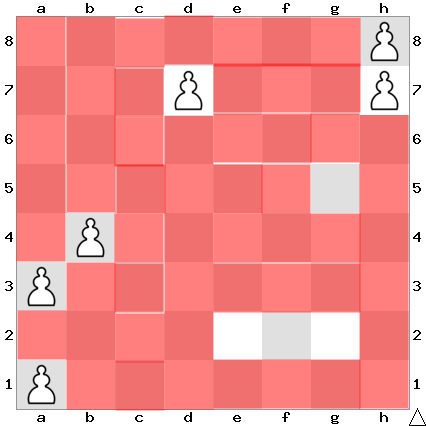
4 is the correct answer.

The question is "how many positions the queen cannot attack any of the pieces?"

Hence, the answer is "4".

Choice C is the correct answer.