CAT Questions | CAT LR DI

CAT DI LR section has become increasingly tough beginning from 2015. However, Understanding the basics of Bar graphs, Pie Charts, Multiple graphs, Line Graphs etc forms an integral part of solving tougher CAT level DI LR questions for the CAT Exam. This question is from CAT 2017 Slot 1 CAT DILR.

CAT DILR : 2017 slot 1 questions

Simple Happiness Index

Simple Happiness index (SHI) of a country is computed on the basis of three parameters: social support (S), freedom to life choices (F) and corruption perception (C). Each of these three parameters is measured on a scale of 0 to 8 (integers only). A country is then categorized based on the total score obtained by summing the scores of ail the three parameters, as shown in the following table:



Following diagram depicts the frequency distribution of the scores in S, F and C of 10 countries - Amda, Benga, Calla, Delma, Eppa, Varsa, Wanna, Xanda, Yanga and Zooma:



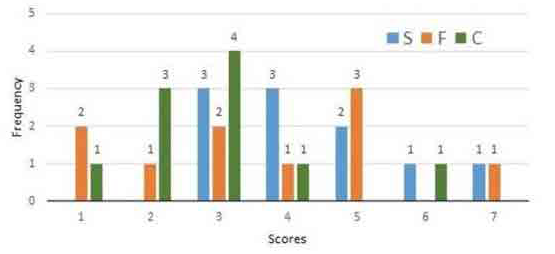
Further, the following are known:
1.Amda and Calla jointly have the lowest total score, 7, with identical scores in all the three parameters.
2.Zooma has a total score of 17.
3.All the 3 countries, which categorised as happy, have the highest score in exactly one parameter.

Question 4: If Benga scores 16 and Delma scores 15, then what is the maximum number of countries with a score of 13?

1. 0
2. 1
3. 2
4. 3

Video Explanation

Explanatory Answer

Method of solving this Question on CAT DILR

General Solution

Some simple inferences
1. No one has got any 8 or 0.
2. Score of 3 is the most frequent, scores of 4 and 5 come right after that.



Now, let us look at some of the constraints
Total adding up to 7 – this can be {1, 1, 5}, {1, 2, 4}, (1, 3, 3), {2, 2, 3} in some order.
A and C get identical scores. So, if one gets {1, 1, 5}, the other also should have got {1, 1, 5}.
We do not even have four 1’s, so {1, 1, 5} is ruled out.
We have 1 two from F, and 3 twos from C. So, we cannot have {2, 2, 3} either. Both A and C could have got a 2 with C, but they both could not have gotten a score of 2 with F.
Both {1, 2, 4} and {1, 3, 3} are possible.
Only F = 1 is possible. Only C = 2 is possible. So, more specifically, we have two possibilities





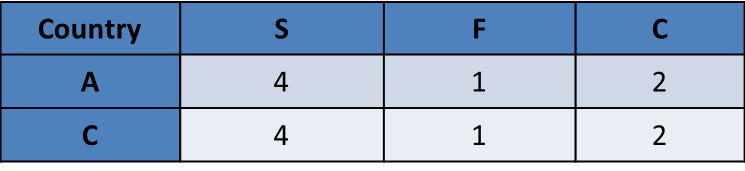
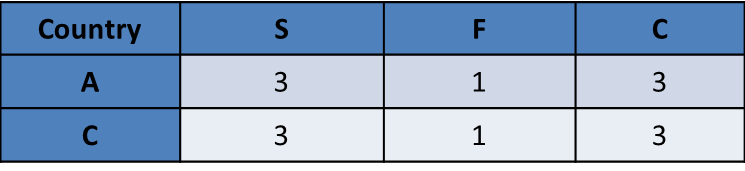
Total adding up to 17 – this can be {7, 6, 4}, {7, 5, 5} or {6, 6, 5} in some order.
Z cannot be {7, 5, 5}.
Why not? Think about this
Only S and F have scores of 7 and 5. There is no C score or 7 or 5. So, Z has to be either {7, 6, 4} or {6, 6, 5}.

Z has to be either {7, 6, 4} or {6, 6, 5}. One Country should have scored highest in S, one in F and one in C. All three totals add up to 14 or more.
Let us call the three as happy Countries as Z, T1, T2 and build possible scenarios.
Let us start with Z = {7, 6, 4}. In this case, Z should have scored the highest in S or F. So some other Country should have scored the highest in C. So, some other Country gets C = 6, Z should get S = 6. So, Z should have got F = 7

Let us start with Z = {7, 6, 4}. In this case, Z should have scored the highest in S or F. So some other Country should have scored the highest in C. So, some other Country gets C = 6, Z should get S = 6. So, Z should have got F = 7. T1 should have S = 7, and T2 should have C = 6



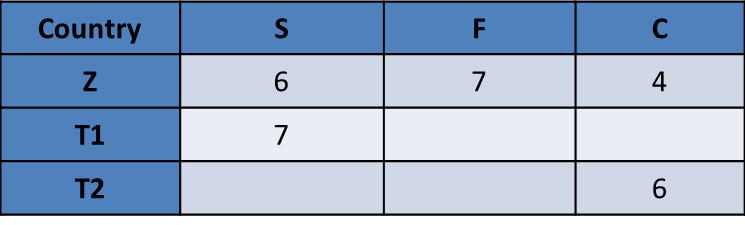
Alternatively Z = {6, 6, 5}. In this case, Z should have scored the highest in C. So the other two Countries should have scored the highest in S and F. Both these tables appear possible.



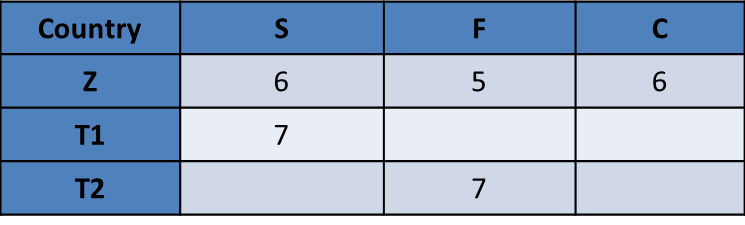
Incorporating all possibilities









Z scores 17, A and C score 7 each. If B and score 16 and 15. The big 3 would account for a total of 48 points. A and C account for 14. A, B, D, A and C account for 62 in total. The total number of points is 109. So, the other 5 should account for 47. If there are 2 13’s, the other 3 should add up to 21. We already have two that add up to 7 each. Having three more that add up to 21 totally is impossible. So, we cannot have 2 or more tied at 13. So, we can either have one team at 13 or two teams at 13. Let us see if we can squeeze in one team at 13. Let us first outline 17, 16, 15 for the big 3 and then build from there.

T1 and T2 being 16 and 15. In all settings we are out of 7’s and 6’s. But this scenario seems possible.

Now, we need to have a T3 that gets to a total of 13. Let us try one at a time. We do not have 6s or 7s. So, we can get 13 as {5, 5, 3} or {5, 4, 4}. {5, 4, 4} is not possible as we do have C = 5 or 4 remaining. But {5, 5, 3} appears possible.



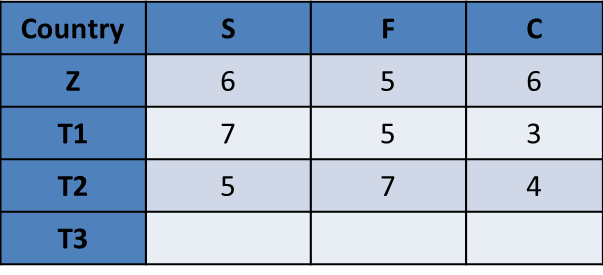
So, we can have a maximum of 1 Country that can have a score of 13.

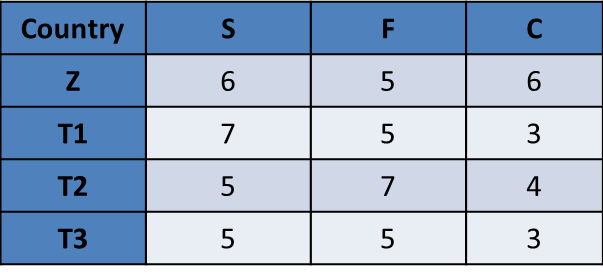
The question is "If Benga scores 16 and Delma scores 15, then what is the maximum number of countries with a score of 13?"

Hence, the answer is "1".

Choice B is the correct answer.