CAT Questions | CAT LR DI

CAT DI LR section has become increasingly tough beginning from 2015. However, Understanding the basics of Bar graphs, Pie Charts, Multiple graphs, Line Graphs etc forms an integral part of solving tougher CAT level DI LR questions for the CAT Exam. This question is from CAT 2017 Slot 1 CAT DILR.

CAT DILR : 2017 slot 1 questions

Common Entrance Test

Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections: Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.

For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1.No one is below the 80th percentile in all 3 sections.
2.150 are at or above the 80th percentile in exactly two sections.
3.The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.

BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.

Question 4: If the number of candidates who are at or above the 90th percentile overall and also are at or above the 80th percentile in P in CET, is more than 100, how many candidates had to sit for the separate test for BIE?

1. 299
2. 310
3. 321
4. 330

Video Explanation

Explanatory Answer

Method of solving this Question on CAT DILR

General Solution

For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1. No one is below the 80th percentile in all 3 sections.
2. 150 are at or above the 80th percentile in exactly two sections.



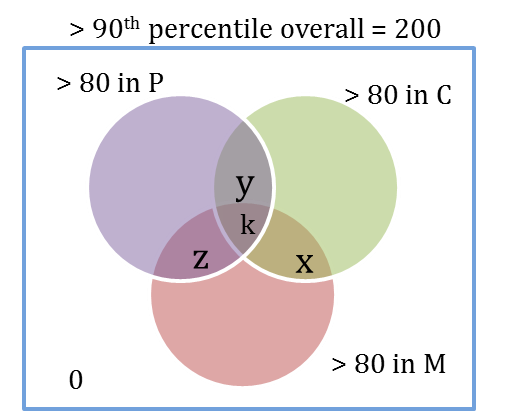
The number outside the three circles is 0
x + y + z = 150

3.The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.
P only, C only and M only = Let each of these be ‘a’.



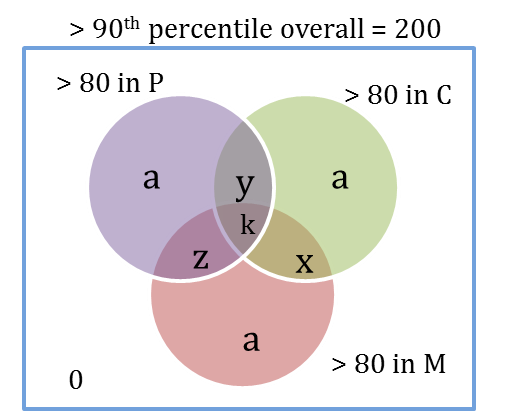
We know that 3a+ k = 50. Overall, there are 200, we know x + y + z = 50. So, 3a + k = 50. Or, k = 50 – 3a.
Number of candidates less than 80 in P = 2a + x
Number of candidates less than 80 in C = 2a + z
Number of candidates less than 80 in M = 2a + y

2a + x : 2a + z : 2a + y = 4 : 2 : 1
Or, 2a + x = 4m, 2a + z = 2m, 2a + y = m.
6a + x + y + z = 7m.
Or, 6a + 150 = 7m. We know that a is less than 17 as 3a + k = 50.

And we know that 6a + 150 is a multiple of 7. Trial and error gives us that a could be 3 or 10. If a were 3, then m would be 24. if a were 10, m would be 30.
If a were 3, we would get a diagram like the one shown adjacent.
x would be 4m - 2a = 4 * 24 – 6 = 90
z would be 2m – 2a = 2 * 24 – 6 = 42
y would be m – 2a = 24 – 6 = 18. These three add up to 150

If a were 10, we would get a diagram like the one shown adjacent.
x would be 4m - 2a = 4 * 30 – 20 = 100
z would be 2m – 2a = 2 * 30 – 20 = 40
y would be m – 2a = 30 – 20 = 10.
These three add up to 150
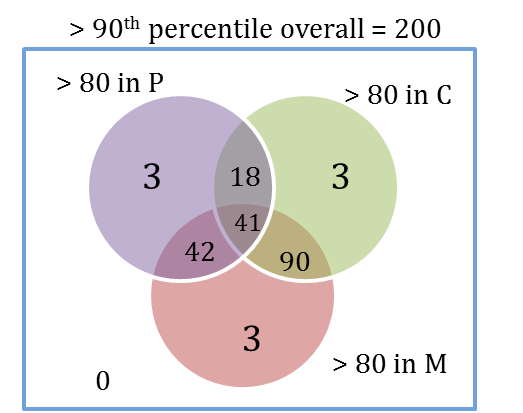
If the number of candidates who are at or above the 90th percentile overall and also are at or above the 80th percentile in P in CET, is more than 100. This tells us that only one diagram is possible – one where the middle number is 41.
In this case, there are 41 + 42 + 18 + 3 = 104 students who have secured more than 80 percentile in P.
Of, the 400 who had scored above 80th percentile the remaining 400-104 = 296 have to take the BIE.
Apart from this, 3 more who have secured >80 in P only also have to take the BIE because they are not eligible to take the AIE. 296 + 3 = 299.

The question is "how many candidates had to sit for the separate test for BIE?"

Hence, the answer is "3 or 10".

Choice A is the correct answer.