CAT Questions | CAT LR DI
CAT DILR | CAT Previous year questions
CAT DI LR section has become increasingly tough beginning from 2015. However, Understanding the basics of Bar graphs, Pie Charts, Multiple graphs, Line Graphs etc forms an integral part of solving tougher CAT level DI LR questions for the CAT Exam. This question is from CAT 2017 Slot 1 CAT DILR.
CAT DILR : 2017 slot 1 questions
Common Entrance Test
Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections: Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1.No one is below the 80th percentile in all 3 sections.
2.150 are at or above the 80th percentile in exactly two sections.
3.The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
Question 2: If the number of candidates who are at or above the 90th percentile overall and also at or above the 80th percentile in all three sections in CET is actually a multiple of 5, what is the number of candidates who are at or above the 90th percentile overall and at or above the 80th percentile in both P and M in CET? (TITA)
Best CAT Online Coaching
Try upto 40 hours for free
Learn from the
best!
2IIM : Best Online CAT Coaching.
Video Explanation
Best CAT Coaching in Chennai
CAT Coaching in Chennai - CAT 2022
Limited Seats Available - Register Now!
Explanatory Answer
Method of solving this Question on CAT DILR
General Solution
For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1. No one is below the 80th percentile in all 3 sections.
2. 150 are at or above the 80th percentile in exactly two sections.
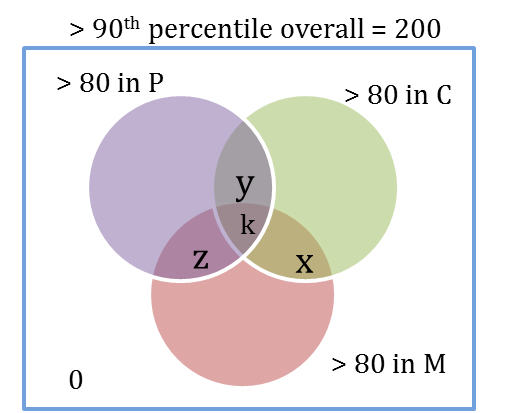
The number outside the three circles is 0
x + y + z = 150
3.The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.
P only, C only and M only = Let each of these be ‘a’.

We know that 3a+ k = 50. Overall, there are 200, we know x + y + z = 50. So, 3a + k = 50. Or, k = 50 – 3a.
Number of candidates less than 80 in P = 2a + x
Number of candidates less than 80 in C = 2a + z
Number of candidates less than 80 in M = 2a + y
2a + x : 2a + z : 2a + y = 4 : 2 : 1
Or, 2a + x = 4m, 2a + z = 2m, 2a + y = m.
6a + x + y + z = 7m.
Or, 6a + 150 = 7m. We know that a is less than 17 as 3a + k = 50.
And we know that 6a + 150 is a multiple of 7. Trial and error gives us that a could be 3 or 10. If a were 3, then m would be 24. if a were 10, m would be 30.
If a were 3, we would get a diagram like the one shown adjacent.
x would be 4m - 2a = 4 * 24 – 6 = 90
z would be 2m – 2a = 2 * 24 – 6 = 42
y would be m – 2a = 24 – 6 = 18. These three add up to 150
If a were 10, we would get a diagram like the one shown adjacent.
x would be 4m - 2a = 4 * 30 – 20 = 100
z would be 2m – 2a = 2 * 30 – 20 = 40
y would be m – 2a = 30 – 20 = 10.
These three add up to 150
The intersection of all three should be a multiple of 5.
This tells us that the intersection value should be 20. Or, we have the second venn diagram.
The number with both P and M = 40 + 20 = 60.
Note that we have to add the 20 also.

The question is "what is the number of candidates who are at or above the 90th percentile overall and at or above the 80th percentile in both P and M in CET?"
Hence, the answer is "60".
CAT Preparation Online | Logical Reasoning for CAT questions Videos On YouTube
CAT Preparation Online | Data Interpretation for CAT questions Videos On YouTube
CAT Questions | CAT Quantitative Aptitude
CAT Questions | CAT DILR
CAT Questions | Verbal Ability for CAT
Copyrights © All Rights Reserved by 2IIM.com - A Fermat Education Initiative.
Privacy Policy | Terms & Conditions
CAT® (Common Admission Test) is a registered trademark of the Indian
Institutes of Management. This website is not endorsed or approved by IIMs.
Where is 2IIM located?
2IIM Online CAT Coaching
A Fermat Education Initiative,
58/16, Indira Gandhi
Street,
Kaveri Rangan Nagar, Saligramam, Chennai 600 093
How to reach 2IIM?
Phone: (91) 44 4505 8484
Mobile: (91) 99626 48484
WhatsApp: WhatsApp Now
Email: prep@2iim.com



