CAT Questions | CAT LR DI
Logical Reasoning for CAT | LR: Visualisation
CAT DI LR section has become increasingly tough beginning from 2015. However, Understanding the basics of Bar graphs, Pie Charts, Multiple graphs, Line Graphs etc forms an integral part of solving tougher CAT level DI LR questions for the CAT Exam. This question is from DATA Interpretation for CAT - Bar Graphs.
Logical Reasoning for CAT: LR Visualisation
A large cube, of total volume 512 3 is made up of smaller 1 cm3 cubes. The larger cube is made by following these rules:
1. Start from the left hand side, and number the small cubes 1 to 8, from left to right.
2. Place cube no. 9 behind cube no. 1 to start the second row, and proceed all the way to cube no. 64
3. Start the second layer on top of cube no 1, and build the second layer from left to right, and front to back like the first layer.
Question 1: On the bottom-most square layer of the cube, consider the surface diagonal that has the square numbered 8, find the sum of all the numbers on the cubes on this surface diagonal on the bottom-most layer.
⏳ Enroll Now for PGDBA – Special Offer Available
2IIM : Best Online CAT Coaching.
Video Explanation
Best CAT Coaching in Chennai
CAT Coaching in Chennai - CAT 2022
Limited Seats Available - Register Now!
Explanatory Answer
Method of solving this Question on Logical Reasoning for CAT:
General Solution:
The first layer of the cube looks like this:
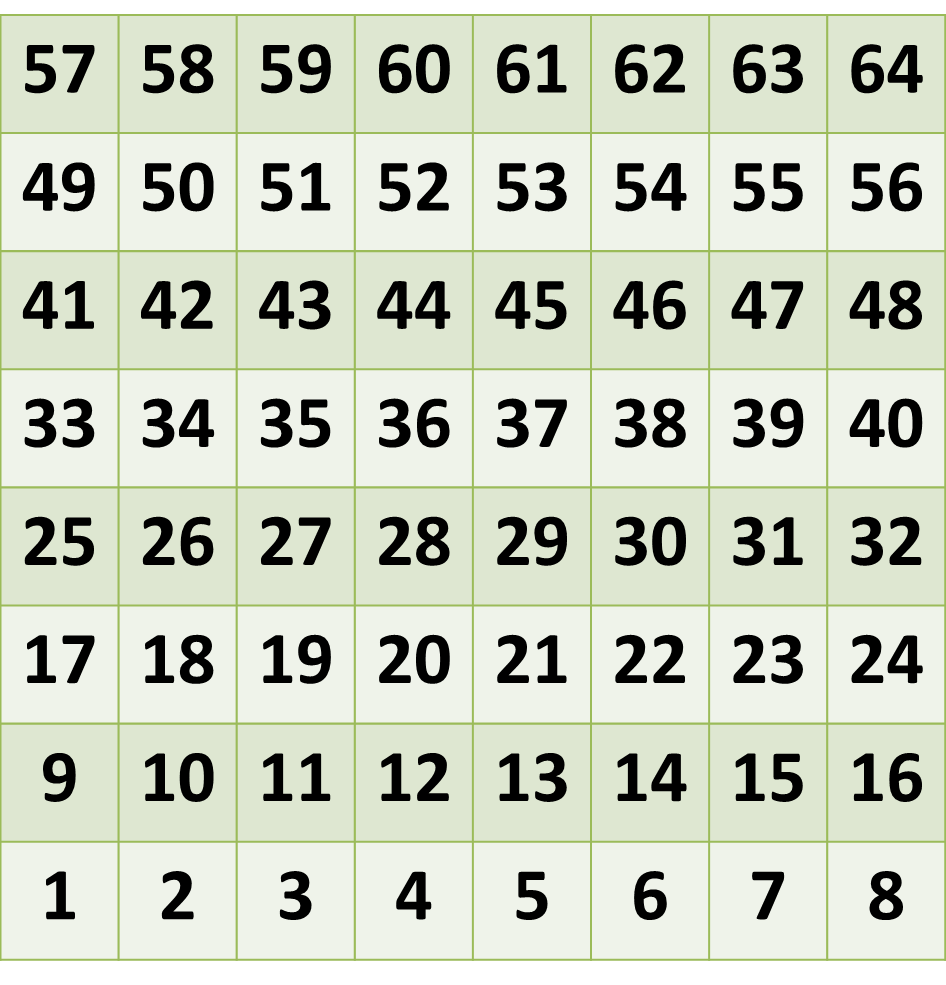
We notice that each of the cubes in the second layer will be 64 + n, where n is the small cube directly below the cube in question. Each of the cubes in the third layer will be 64 x 2 + n, and so on.
In general, to find the number on a particular cube 'P' on the k'th layer, we can use the formula P = (k - 1)x64 + n, where n is the number on the bottom-most cube below P. With this general idea, we can solve the whole puzzle.
Solution for Question 1:
Since this diagonal is on the bottom-most layer, we can refer to the diagram above. Clearly the diagonal is made up of numbers forming an arithmetic progression, where the first term is 8, and the common difference is 7. There are 8 terms in all. We can find the sum of all the numbers using the AP formula:
Sum=(2a+(n−1)d)\\frac{n}{2}\\)
Sum=(2×8+7×7)×4=260
The question is "find the sum of all the numbers on the cubes on this surface diagonal on the bottom-most layer."
Hence, the answer is "260".
CAT Preparation Online | Logical Reasoning for CAT questions Videos On YouTube
CAT Preparation Online | Data Interpretation for CAT questions Videos On YouTube
CAT Questions | CAT Quantitative Aptitude
CAT Questions | CAT DILR
CAT Questions | Verbal Ability for CAT
Copyrights © All Rights Reserved by 2IIM.com - A Fermat Education Initiative.
Privacy Policy | Terms & Conditions
CAT® (Common Admission Test) is a registered trademark of the Indian
Institutes of Management. This website is not endorsed or approved by IIMs.
Where is 2IIM located?
2IIM Online CAT Coaching
A Fermat Education Initiative,
19/43, MG Chakrapani St,
Sathya Garden, Saligramam, Chennai 600 093
How to reach 2IIM?
Phone: (91) 44 4505 8484
Mobile: (91) 99626 48484
WhatsApp: WhatsApp Now
Email: prep@2iim.com



