CAT Questions | CAT LR DI
Logical Reasoning for CAT | LR: Patterns
CAT DI LR section has become increasingly tough beginning from 2015. However, Understanding the basics of Bar graphs, Pie Charts, Multiple graphs, Line Graphs etc forms an integral part of solving tougher CAT level DI LR questions for the CAT Exam. This question is from Logical Reasoning for CAT - Patterns.
Logical Reasoning for CAT: Patterns
Imperialist Gold Diggers
A group of six imperialists Alpha, Omega, Beta, Theta, Phi and Delta carve out a circle in Antartica and break it up into six sectors. There are 48 Gold mines spread across this circle that covers an area of 3600 sq kms.
Beta and Phi got the same area, while Theta and Delta got the same area. Area of Beta, Delta and Omega form an Arithmetic Progression with Delta being the middle term. Areas of Omega, Beta and Alpha form a Geometrics Progression with Beta being the middle term. The number of goldmines of Delta, Omega, Beta, Alpha and Theta form an Arithmetic Progression in that order. As many Countries have got more goldmines than Phi as have got fewer goldmines than Phi.
One has to cross at least two other Countries to go from Alpha to Delta; there is only one Country to cross between Phi and Omega; and Alpha and Beta are neighboring Countries. The Country that has got the maximum number of goldmines has an area of 450 sq kms, the Country that has got the maximum area has got 6 gold mines. Omega has lesser area than his neighbor Beta and Phi has got more goldmines than his neighbor Theta.
Question 4: Which imperialist got the region between Phi and Omega?
🎉Pongal Offer: Get up to ₹20,000 off on CAT 2026 courses (Valid from January 13–17).
2IIM : Best Online CAT Coaching.
Best CAT Online Coaching
Try upto 40 hours for free
Learn from the
best!
2IIM : Best Online CAT Coaching.
Video Explanation
Best CAT Coaching in Chennai
CAT Coaching in Chennai - CAT 2022
Limited Seats Available - Register Now!
Explanatory Answer
Method of solving this Question on Logical Reasoning for CAT
General Solution
As ever, let us make some sense of the constraints and then draw a table or graph.
Areas - Beta = Phi = X, Theta = Delta = Y.
Area of Beta, Delta and Omega form an Arithmetic Progression with Delta being the middle term.
X, Y and Omega form an AP. Or, Omega = 2Y – X
Areas of Omega, Beta and Alpha form a Geometrics Progression with Beta being the middle term. Or, 2Y – X, X and Alpha form a GP.
Alpha = \\frac{X^2}{2Y - X}\\)
Now, let us move to the goldmines:
As many Countries have got more goldmines than Phi as have got fewer goldmines than Phi. There are totally 6 Countries, so Phi cannot be the lone middle term. So, Phi has to be joint third. So, we should have number of goldmines as P < Q < R=R < S < T.
Now, we know that the number of goldmines of Delta, Omega, Beta, Alpha and Theta form an Arithmetic Progression in that order. So, the number of goldmines of Beta and Phi should be same, say R. Then we have R – 2d, R- d, R, R, R + d, R + 2d. The sum of all these is 6R. Or, R = 8.
So, Phi and Beta have 8 goldmines each.
Now, let us create a table and work from there
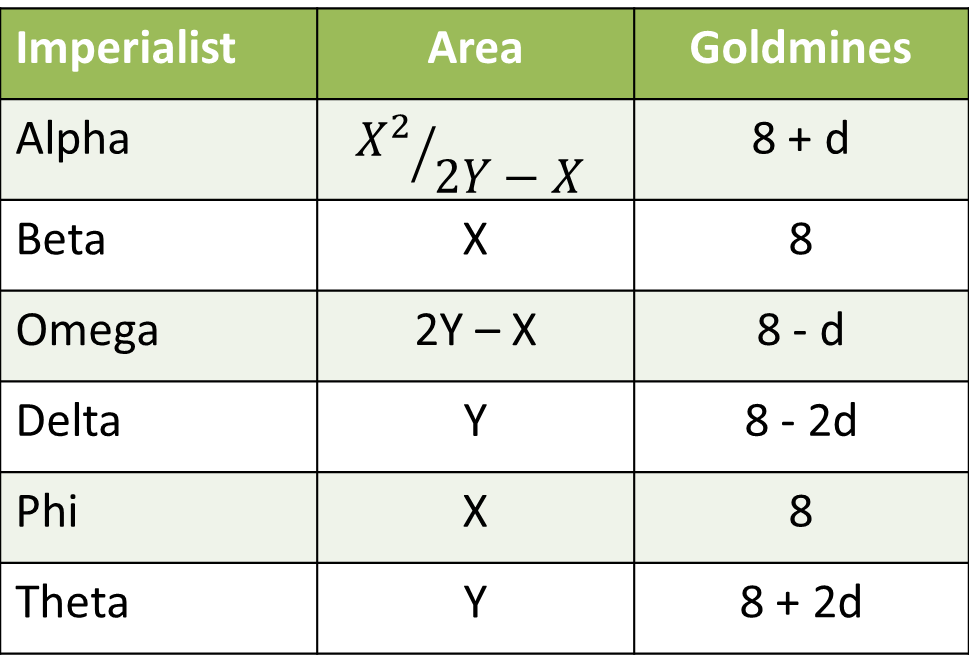
Omega has lesser area than his neighbor Beta . Or, 2Y – X < X. Or, Y < X.
and Phi has got more goldmines than his neighbor Theta. Or, d < 0.
8 + d and 8 + 2d should be less than 8, whereas 8 – d and 8 – 2d should be higher than 8. The Country that has got the maximum number of goldmines has an area of 450 sq kms. Or, Delta has an aread of 450 sq kms. Y = 450 sq kms.
The Country that has got the maximum area has got 6 gold mines. Alpha or Theta should have 6 gold mines.
Now, we know Y < X. So, Theta does not have the maximum area. So, alpha should have the maximum area. SO, 8 + d=6. Or, d=-2. We have cracked the goldmine part completely. Let us include this in our table.

Total area is 3600 sq kms. Or, \\frac{X^2}{900 - X}\\) + X + 900 +X + 450+X + 450 = 3600.
Or \\frac{X^2}{900 - X}\\) + X = 1800
X2 +900X -X2 =1800(900-X)
Solving, we get X = 600, so 900 - X = 300.
The table now looks like:

Now, let us move on to the positions on the grid. One has to cross at least two other Countries to go from Alpha to Delta – Alpha and Delta are diametrically opposite to each other ( athough the sectors might have different areas) Alpha and Beta are neighboring Countries. Omega has lesser area than his neighbor Beta. Or, Beta sits between Alpha and Omega. So, we have Alpha, Beta, Omega in a sequence.
Alpha and Delta are diametrically across. So, we should have Alpha, Beta, Omega and Delta in a sequence.
There is only one Country to cross between Phi and Omega. One Country removed from Omega in one direction is Alpha. In the other direction it should be Phi. So, we should have Alpha, beta, Omega, Delta, Phi in a sequence.
Phi has got more goldmines than his neighbor Theta.
Or, the sequence is Alpha, Beta, Omega, Delta, Phi, Theta.
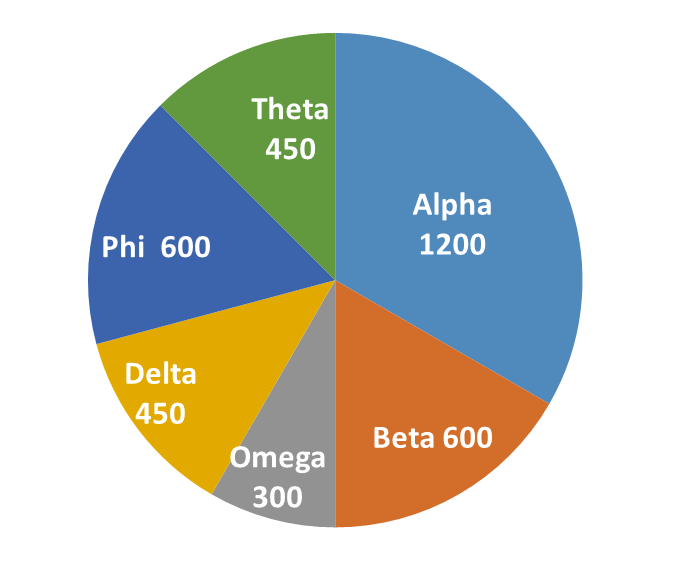
From the chart, the answer is Delta.
The question is "Which imperialist got the region between Phi and Omega?"
Hence, the answer is "Delta".
CAT Preparation Online | Logical Reasoning for CAT questions Videos On YouTube
CAT Preparation Online | Data Interpretation for CAT questions Videos On YouTube
CAT Questions | CAT Quantitative Aptitude
CAT Questions | CAT DILR
CAT Questions | Verbal Ability for CAT
Copyrights © All Rights Reserved by 2IIM.com - A Fermat Education Initiative.
Privacy Policy | Terms & Conditions
CAT® (Common Admission Test) is a registered trademark of the Indian
Institutes of Management. This website is not endorsed or approved by IIMs.
Where is 2IIM located?
2IIM Online CAT Coaching
A Fermat Education Initiative,
58/16, Indira Gandhi
Street,
Kaveri Rangan Nagar, Saligramam, Chennai 600 093
How to reach 2IIM?
Phone: (91) 44 4505 8484
Mobile: (91) 99626 48484
WhatsApp: WhatsApp Now
Email: prep@2iim.com



