CAT Questions | CAT LR DI

Solve this DILR Question on Tea Tasting from CAT 2017. You are expected to answer the questions that follow, based on the constraints given. Some constraints could be specific to each question. If you would like to take these questions as a Quiz, head on here to take these questions in a test format, absolutely free.

CAT DILR : 2017 slot 2 questions

Tea Tasting

A tea taster was assigned to rate teas from six different locations - Munnar, Wayanad, Ooty, Darjeeling, Assam and Himachal. These teas were placed in six cups, numbered 1 to 6, not necessarily in the same order. The tea taster was asked to rate these teas on the strength of their flavour on a scale of 1 to 10. He gave a unique integer rating to each tea.
Some other information is given below:
1. Cup 6 contained tea from Himachal.
2. Tea from Ooty got the highest rating, but it was not in Cup 3.
3. The rating of tea in Cup 3 was double the rating of the tea in Cup 5.
4. Only two cups got ratings in even numbers.
5. Cup 2 got the minimum rating and this rating was an even number.
6. Tea in Cup 3 got a higher rating than that in Cup 1.
7. The rating of tea from Wayanad was more than the rating of tea from Munnar, but less than that from Assam.

Question 4: If the tea from Munnar did not get the minimum rating, what was the rating of the tea from Wayanad?

1. 3
2. 5
3. 1
4. 6

Video Explanation

Explanatory Answer

Method of solving this Question on CAT DILR

General Solution

Let us start by making some sense of the given data.
From statement 4, only two cups have been given even numbered ratings and one of them is given to the tea in Cup 2 (from statement 5).
From statement 3, it can be inferred that the rating of the tea in Cup 3, is an even number as the rating of the tea in Cup 3 is double the rating of the tea in cup 5.
If Cup 5 has a rating of x, then cup 3 has rating of 2x, which is always even.
We also know that the rating of the tea in Cup 5 is an odd number.
So cups 3 and 5 could have ratings 1 & 2, 3 & 6, or 5 & 10. Cup 2 has the least rating and so Cup 5 cannot have 1. So, cups 3 & 5 could have ratings 3 & 6, or 5 & 10. Cup 3 does not have the highest rating, so we can say Cup 5 has rating of 3 and Cup 3 has a rating of 6.

From statement 5, the rating of the tea in Cup 2 can either be 2 or 4. It cannot go above that because then, the rating of cup 5 will be 7 and rating of cup 3 will 2*7 = 14 which is not possible. But can Cup 2 really be as high as 4?

If the rating of the tea in Cup 2 is 4, the minimum possible rating for the tea in Cup 5 will be 5. Hence, the rating of the tea in Cup 3 will be 10. But cup 3 does not have the highest rating and the ratings are all unique.
Therefore, the tea in Cup 2 has a rating of 2.

Cup5 has a rating of 3 and Cup 3 has a rating of 6.

From statement (6), we can say that Cup 1 < Cup 3 . Rating of Cup 1 cannot be 1 and 3. It also cannot 4 as the number of even integer ratings is only 2. Hence, Cup 1 has a rating of 5.

So, story so far ===> Cup 1 = Rating of 5, Cup 2 = Rating of 2, Cup 3 = Rating of 6, Cup 5 = Rating of 3. The only possible remaining ratings are 7 and 9. Cups 4 and 6 should have these two ratings in some order.

Cup 6 is Himachal and Ooty has the highest rating, so Cup 6’s rating is 7 as the cup containing tea from Ooty has to be Cup 4.
Let us now create a table:



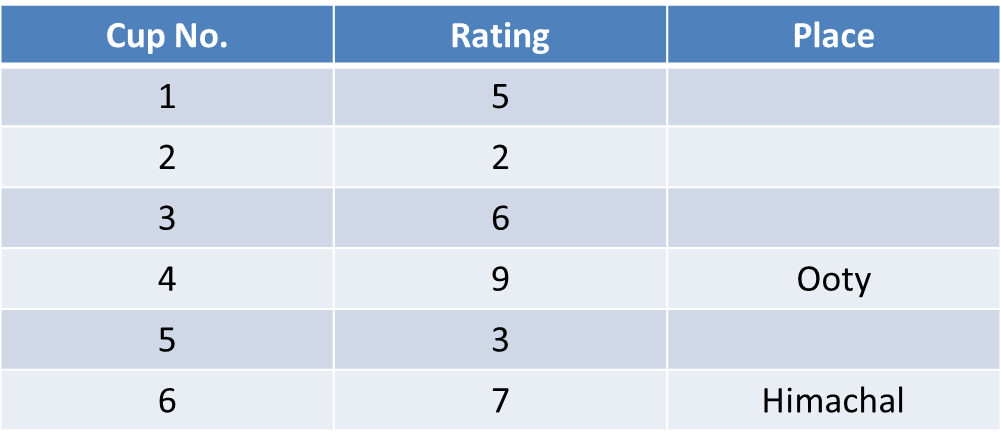
We also know that rating of Assam > Wayanad > Munnar

The cup no.’s that are still unassigned to the places are Cup1, 2, 3 and 5.

Now, among these four tea from Munnar can either be in Cup 2 or Cup 5. If the tea from munnar does not have the lowest rating, then it has a rating of 3 and hence it is in Cup 5.
We know, rating of Assam > Wayanad > Munnar . Hence, if Munnar has a rating of 3, then, Wayanad should have a rating of 5 and Assam should have rating of 6.

Hence, Wayanad has a rating of 5

The question is "If the cup containg teas from Wayanad and Ooty had consecutive numbers, which of the given may be true ?"

Hence, the answer is " Cup 1 contains tea from Darjeeling".

Choice B is the correct answer.