CAT Quantitative Aptitude Questions | CAT Time Speed and Distance & Races

CAT Questions

The question is from the topic Time and distance. It is a classic question involving the concept of speed, distance and time. Time Speed and Distance is a favorite in CAT Exam, and appears more often than expected in the CAT Quantitative Aptitude section in the CAT Exam

Question 3: Three cars leave A for B in equal time intervals. They reach B simultaneously and then leave for Point C which is 240 km away from B. The first car arrives at C an hour after the second car. The third car, having reached C, immediately turns back and heads towards B. The first and the third car meet a point that is 80 km away from C. What is the difference between the speed of the first and the third car?

1. 60 kmph
2. 20 kmph
3. 40 kmph
4. 80 kmph

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Time Speed Distance: Create a visual of where the three cars are and how they travel between the points.

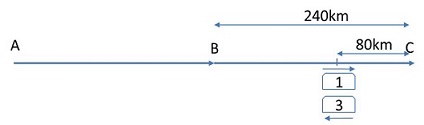
Let V1, V2 and V3 be the speeds of the cars.

\\frac{AB}{V_{1}}\\) - \\frac{AB}{V_{2}}\\) = \\frac{AB}{V_{2}}\\) - \\frac{AB}{V_{3}}\\)
\\frac{240}{V_{1}}\\) - \\frac{240}{V_{2}}\\) = 1
V₃ = 2V₁

Condition I states that the cars leave in equal intervals of time and arrive at the same time. Or, the difference in the time taken between cars 1 and 2 should be equal to the time taken between cars 2 and 3.

We get \\frac{AB}{V_{1}}\\) - \\frac{AB}{V_{2}}\\) = \\frac{AB}{V_{2}}\\) - \\frac{AB}{V_{3}}\\)
As the second car arrived at C an hour earlier than the first, we get a second equation
\\frac{240}{V_{1}}\\) - \\frac{240}{V_{2}}\\) = 1
The third car covered 240 + 80 kms when the first one covered 240 – 80 kms. Therefore, \\frac{320}{V_{3}}\\) = \\frac{160}{V_{1}}\\)
This gives us V₃ = 2V₁
From condition 1, we have \\frac{AB}{V_{1}}\\) - \\frac{AB}{V_{2}}\\) = \\frac{AB}{V_{2}}\\) - \\frac{AB}{V_{3}}\\)
Substituting V₃ = 2V₁, this gives us \\frac{AB}{V_{1}}\\) - \\frac{AB}{V_{2}}\\) = \\frac{AB}{V_{2}}\\) - \\frac{AB}{2V_{1}}\\)
or \\frac{3AB}{2V_{1}}\\) = \\frac{2AB}{V_{2}}\\) or V₂ = \\frac{4V_{1}}{3}\\)
Solving \\frac{240}{V_{1}}\\) - \\frac{240}{V_{2}}\\) = 1 , we get \\frac{60}{V_{1}}\\) = 1 or V₁ = 60 kmph
=> V₂ = 80 kmph and V₃ = 120 kmph

The question is "What is the difference between the speed of the first and the third car?"

Hence, the answer is 60 kmph

Choice A is the correct answer.