CAT Quantitative Aptitude Questions | CAT Time Speed and Distance & Races

CAT Questions

The question is from the topic time and distance. Time taken while increasing and decreasing speed is given, we need to find out the distance. Time Speed and Distance is a favorite in CAT Exam, and appears more often than expected in the CAT Quantitative Aptitude section in the CAT Exam

Question 22 : Akash when going slower by 15 Km/hr, reaches late by 45 hours. If he goes faster by 10 Km/hr from his original speed, he reaches early by 20 hours than the original time. Find the distance he covers.

1. 8750 Km
2. 9750 Km
3. 1000 Km
4. 3750 Km

---

---

---

---

Explanatory Answer

Method of solving this CAT Question from Time Speed Distance: Knowing the relationship between speed and distance would help.

You may solve for D and S by writing the equations as:
\\frac{D}{s−15}\\) − \\frac{D}{s}\\) = 45
\\frac{D}{s}\\) - \\frac{D}{s+10}\\) = 20
You can solve these two equations to get D = 9750 Km which is a perfectly fine approach. However, if you are comfortable with alligation, you may save time on such TSD question as:

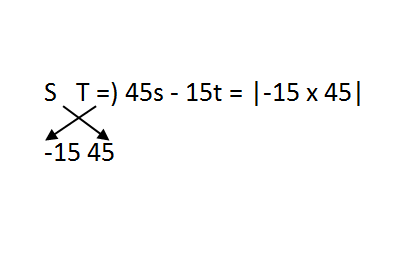
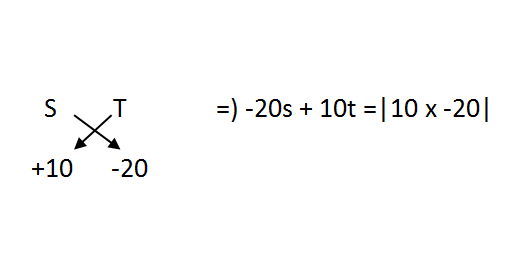
Both these equations can be solved quickly to get s = 65 Km/hr, t = 150 hr. Therefore, D = 9750 Km. I want to reiterate that using the first approach is perfectly fine. That's how I would do it. It is better to spend 20 seconds extra and get the right answer instead of getting it wrong with something you are not comfortable with.

Alternate Solution:
Let the normal speed be s
and the normal time be t

The distance D = st.

When speed decreases by 15 kmph, time increases by 45 hours. The distance will still be the same.
D = (s-15)(t+45)
st = (s-15)(t+45)
st = st +45s - 15t - 15*45
45s - 15t - 15*45 = 0
3s -t -45 = 0
3s = t + 45
t = 3s - 45

When speed increases by 10 kmph, time decreases by 20 hours. The distance will still be the same.

D = (s+10)(t-20)
st = (s+10)(t-20)
st = st -20s + 10t - 10*20
-20s + 10t - 10*20 = 0
-2s +t -20 = 0
t = 20 + 2s

So, t = 3s - 45 and t = 20 + 2s
3s - 45 = 20 + 2s
s = 65

So speed = s = 65 kmph
t = 20 + 2s
time = t = 20 + 2*65 = 150
Distance = st = 65 * 150 = 9750 km

The question is "Find the distance he covers."

Hence, he covers 9750 km.

Choice B is the correct answer.