CAT Quantitative Aptitude Questions | CAT Time Speed and Distance & Races

CAT Questions

The question is from the topic Races. It also involves ideas from Geometry. CAT exam is known to test on multiple ideas in the same question, so you should be ready to face them. Time Speed and Distance is a favorite in CAT Exam, and appears more often than expected in the CAT Quantitative Aptitude section in the CAT Exam

Question 2: Consider a square ABCD. EFGH is another square obtained by joining the midpoints of the sides of the square ABCD where E, F , G amd H are the midpoints of AB, BC, CD and DA respectively. Lakshman and Kanika start from points B and D respectively at speeds ‘l’ kmph and ‘k’ kmph respectively and travel towards each other along the sides of the square ABCD. Jagadeesh starts from Point E and travels along the Square EFGH in the anti-clockwise direction at ‘j’ kmph. Lakshman and Kanika meet for the second time at H where Jagadeesh also meets them for the first time. If l : k : j is 1: 3 : 5√2 then the distance travelled by Jagadeesh is

1. 7.5 × √2 times the side of the square ABCD
2. 7.5 × √2 times the side of the square EFGH
3. 7.5 times the side of the square ABCD
4. 7.5 times the side of the square EFGH

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Races: Lakshman and Kanika meet for the second time at H where Jagadeesh also meets them for the first time √2.

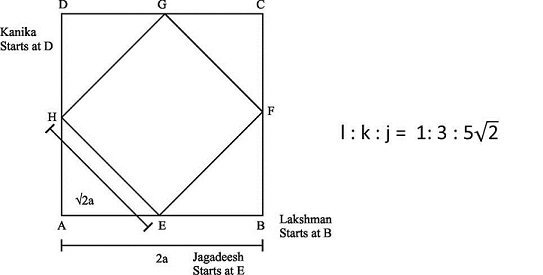
Lakshman and Kanika start from points B and D respectively at speeds ‘l’ kmph and ‘k’ kmph respectively and travel towards each other along the sides of the square ABCD. They are at a distance of 4a from each other. Since they are at diametrically opposite points, the relative distance would be 4a irrespective of the directions they choose to travel in. So, to meet for the first time, they would have travelled a distance of 4a together.

To meet for the second time, they would have travelled a further 8a together. Essentially, between them, they would have to cover the entire perimeter of the square to meet again.

So by the time they meet for the second time, they would have covered a distance of 12a together. Their speeds are in the ratio 1: 3. So, Lakshman would have travelled 3a and Kanika would have travelled 9a.

Or, Lakshman travels in the direction BADC, while Kanika would have travelled in the direction DABC. They meet for the first time at E and the second time at H.

In the same time, Jagadeesh travels along the square EFGH in the anti-clockwise direction at ‘j’ kmph and meets Lakshman and Kanika. While Jagadeesh meets the other two for the first time, we do not know how many laps he has completed by then.

The ratio of Lakshman’s speed to that of Jagadeesh is 1: 5√2 so, they would have travelled distances in the same ratio as well. So, if Lakshman has travelled a distance of 3a, Jagadeesh should have travelled a distance of 3a x 5√2 to reach H.

Or, Jagadeesh travels 52a to reach H. Answer choice (a)

The question is "If l : k : j is 1: 3 : 5√2 then the distance travelled by Jagadeesh is"

Hence, the answer 7.5 × √2 times the side of the square ABCD

Choice A is the correct answer.