CAT Quantitative Aptitude Questions | Geometry Questions for CAT - Triangles

CAT Questions

The question is from CAT Geometry - Triangles. It discusses about an equilateral triangle with a square inscribed inside it. CAT Geometry questions are heavily tested in CAT exam. Make sure you master Geometry problems. This question asks about ratio of area of the square to that of the equilateral triangle.

Question 6: There is an equilateral triangle with a square inscribed inside it. One of the sides of the square lies on a side of the equilateral △. What is the ratio of the area of the square to that of the equilateral triangle?

1. 12 : 12 + 7√3
2. 24 : 24 + 7√3
3. 18 : 12 + 15√3
4. 6 : 6 + 5√3

---

---

Video Explanation

---

---

Explanatory Answer

Method of solving this CAT Question from Triangles: Mathematicians love symmetry, question setters are nearly besotted with it. So, learn about symmetric figures well.

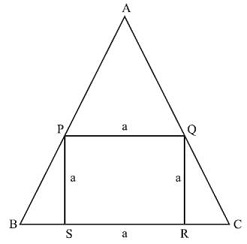
APQ is an equilateral △. As PQ is parallel to BC.
Let side of the square be ‘a’
AP = a = AQ
△QRC has angles 30 – 60 – 90.

\\frac{QR}{QC}\\) = \\frac{√3}{2}\\)
QC = QR * \\frac{2}{√3}\\)
AC = AQ + QC = a + \\frac{2a}{√3}\\)
Area of equilateral △ = \\frac{√3}{4}\\) AC²
= \\frac{√3}{4}\\) (a + \\frac{2a}{√3}\\))²
= \\frac{√3}{4}\\) (\\frac{√3a + 2a}{√3}\\))²
= \\frac{√3}{4}\\) * (\\frac{1}{3}\\)) a²(4 + 3 + 4√3)
= \\frac{7 +4 √3}{12}\\) * √3a²
= \\frac{12 + 7√3}{12}\\) * a²
Ratio of area of square to that of equilateral △ is = a² : \\frac{12 + 7√3}{12}\\) * a²
= 12 : 12 + 7√3

The question is "What is the ratio of the area of the square to that of the equilateral triangle?"

Hence, the answer is 12 : 12 + 7√3.

Choice A is the correct answer.