CAT Quantitative Aptitude Questions | Geometry Questions for CAT - Triangles

The question is from CAT Geometry - Triangles. It discusses about the circles inscribed in the equilateral triangle. CAT Geometry questions are heavily tested in CAT exam. Make sure you master Geometry problems. With the given diagram how could we find the ratio of the inscribed circle to the equilateral triangle

Question 4: Two circles are placed in an equilateral triangle as shown in the figure. What is the ratio of the area of the smaller circle to that of the equilateral triangle

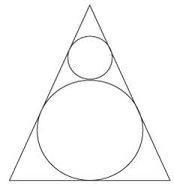
1. π:36√3
2. π:18√3
3. π:27√3
4. π:42√3

Video Explanation

Explanatory Answer

Method of solving this CAT Question from Triangles: A clear understanding of circles, squares and equilateral triangles will help to solve.

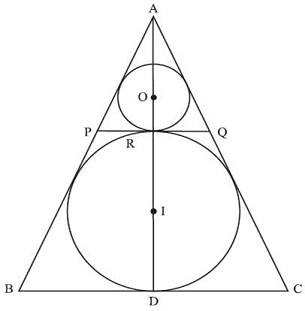
In-radius of equilateral triangle of side a = \\frac{a}{2√3}\\)
Diameter of larger circle = \\frac{a}{2√3}\\)

Let us say common tangent PQ touches the two circle at R, center of smaller circle is I.
Now, PQ is parallel to BC. AR is perpendicular to PQ. Triangle PQR is also an equilateral triangle and AORID is a straight line. (Try to establish each of these observations. Just to maintain the rigour.)

AD = \\frac{√3}{2}\\)a
RD = \\frac{a}{√3}\\)
AR = \\frac{√3}{2}\\)a - \\frac{a}{√3}\\) = \\frac{3a-2a}{2√3}\\) = \\frac{a}{2√3}\\)
AR = \\frac{1}{3}\\) AD
Radius of smaller circle = \\frac{1}{3}\\) radius of larger circle
Radius of smaller circle = \\frac{1}{3}\\) * \\frac{a}{2√3}\\) = \\frac{a}{6√3}\\)
Area of smaller circle = πr²
π (\\frac{a}{6√3}\\))² = \\frac{πa^2}{108}\\)
Area of triangle = \\frac{√3}{4}\\)a²
Ratio = \\frac{πa^2}{108}\\) : \\frac{√3}{4}\\)a² = π:27√3

The question is " What is the ratio of the area of the smaller circle to that of the equilateral triangle?"