CAT Quantitative Aptitude Questions | Geometry Questions for CAT - Triangles
CAT Questions | CAT Geometry Questions | Circles and Triangle
CAT Questions The question is from CAT Geometry - Triangles. It tests our understanding on properties of a triangle. CAT Geometry questions are heavily tested in CAT exam. Make sure you master Geometry problems. In this question it discusses about the properties of area of a triangle.
Question 30: Two circles with centres O1 and O2 touch each other externally at a point R. AB is a tangent to both the circles passing through R. P’Q’ is another tangent to the circles touching them at P and Q respectively and also cutting AB at S. PQ measures 6 cm and the point S is at distance of 5 cms and 4 cms from the centres of the circles. What is the area of the triangle SO1O2?
- 9 cm2
- 3(4+√7)/2 cm2
- 27/2 cm2
- (3√41)/2 cm2
3(4+√7)/2 cm2
Best CAT Online Coaching
Try upto 40 hours for free
Learn from the
best!
2IIM : Best Online CAT Coaching.
Best CAT Coaching in Chennai
CAT Coaching in Chennai - CAT 2022
Limited Seats Available - Register Now!
Explanatory Answer
Method of solving this CAT Question from Triangles: To calculate the area of a triangle, determine its base and altitude!!
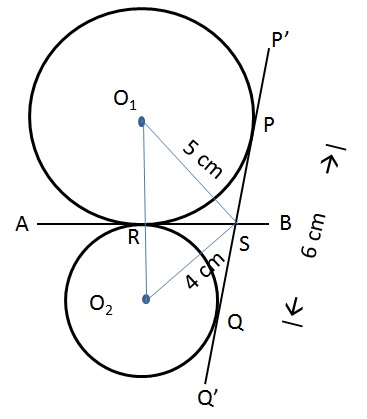
From the diagram we see that SP, SR are tangents to circle1 from same point S. Similarly SR, SQ are tangents from same point to circle 2.
SP = SR; SQ = SR implies SP = SQ
Given PQ = 6cm
SP + SQ = 6
Therefor SR = SP = SQ = 3 cm.
SR is the altitude to the triangle SO1O2. We need to find the length of the base O1O2 to determine the area.
O1RS is a right angled triangle with hypotenuse = 5 and one side = 3
Therefore, O1R = √(52 - 32) = 4cm
Similarly, O2RS is a right angled triangle with hypotenuse = 4 and one side = 3
Therefore, O2R = √(42 - 32) = √7cm
O1O2 = O1R + O2R = 4 + √7
Area of the triangle SO1O2 = 1/2 * SR * O1O2 = 1/2 * 3 * (4 + √7) cm2
The question is " What is the area of the triangle SO1O2?"
Hence, the answer is 3(4+√7)/2 cm2.
Choice B is the correct answer.
