🎉Ace the Final Stretch with our Last Mile Excellence – Your Ultimate CAT 2024 Boost!

CAT Questions | CAT Trigonometry Questions

CAT Quantitative Aptitude | CAT Trigonometry

A CAT Geometry question from the topic - CAT Trigoneometry that appears in the Quantitative Aptitude section of the CAT Exam broadly tests an aspirant on the concepts - Basic Trigonometric Functions, Heights and Distances, Sine rule, Cosine rule etc . In CAT Exam, one can generally expect to get approx. 1 question from CAT Trigonmetry. Make use of 2IIMs Free CAT Questions, provided with detailed solutions and Video explanations to obtain a wonderful CAT score. If you would like to take these questions as a Quiz, head on here to take these questions in a test format, absolutely free.

CAT Geometry: Trigonometric Functions

3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can to take?
1. 5
2. -5
3. 4
4. 3
Choice A
5
CAT Geometry: Trigonometry - Range of Functions

Sin²⁰¹⁴x + Cos²⁰¹⁴x = 1, x in the range of [-5π, 5π], how many values can x take?
1. 0
2. 10
3. 21
4. 11
Choice C
21
CAT Geometry: Trigonometry - Maximum and Minimum Value

Consider a regular hexagon ABCDEF. There are towers placed at B and D. The angle of elevation from A to the tower at B is 30 degrees, and to the top of the tower at D is 45 degrees. What is the ratio of the heights of towers at B and D?
1. 1:√3
2. 1:2√3
3. 1:2
4. 3:4√3
Choice B
1:2√3
CAT Geometry: Trigonometry - Maximum and Minimum Value

Find the maximum and minimum value of 8 cos A + 15 sin A + 15
1. 11√2+15; 15
2. 30; 8
3. 32; -2
4. 23; 8
Choice C
32; -2
CAT Geometry: Trigonometry - Trigonometric Identities

If cos A + cos² A = 1 and a sin¹² A + b sin¹⁰ A + c sin¹⁰ A + d sin⁶ A - 1 = 0. Find the value of a+b/c+d
1. 4
2. 3
3. 6
4. 1
Choice B
3
CAT Geometry: Trigonometry - Trigonometric Identities

In the below figure, the sheet of width W is folded along PQ such that R overlaps S Length of PQ can be written as :-
1. \\frac{w}{sinα(1+cos2α)}\\)
2. \\frac{w}{sin2αcosα}\\)
3. \\frac{w}{1+sin2α}\\)
4. Any two of the above
Choice D
Any two of the above
CAT Geometry: Trigonometry - Trigonometry and Logarithm

Find the value of :- (log sin 1° + log sin 2° ………..+ log sin 89°) + (log tan 1° + log tan 2° + ……… + log tan 89°) - (log cos 1° + log cos 2° + ……… + log cos 89°)
1. \\frac{log√2}{(1+√2)}\\)
2. -1
3. 1
4. None of these
Choice D
None of these
CAT Geometry: Trigonometry - Height and Distances

Ram and Shyam are 10 km apart. They both see a hot air balloon passing in the sky making an angle of 60° and 30° respectively. What is the height at which the balloon could be flying?
1. \\frac{5√3}{2}\\)
2. 5√3
3. Both A and B
4. Cannot be determined
Choice C
Both A and B
CAT Geometry: Trigonometry - Height and Distances

A man standing on top of a tower sees a car coming towards the tower. If it takes 20 minutes for the angle of depression to change from 30° to 60°, what is the time remaining for the car to reach the tower?
1. 20√3 minutes
2. 10 minutes
3. 10√3 minutes
4. 5 minutes
Choice B
10 minutes
CAT Geometry: Trigonometry - Right Triangle

A right angled triangle has a height ‘p’, base ‘b’ and hypotenuse ‘h’. Which of the following value can h2 not take, given that p and b are positive integers?
1. 74
2. 52
3. 13
4. 23
Choice D
23
CAT Geometry: Trigonometry - Trigonometric Identities

If tanϕ + sinϕ = m, tanϕ − sinϕ = n, Find the value of m² - n²
1. 2√mn
2. 4√mn
3. m-n
4. 2mn
Choice B
4√mn
CAT Geometry: Trigonometry - Heights and Distances

A student is standing with a banner at the top of a 100 m high college building. From a point on the ground, the angle of elevation of the top of the student is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the student.
1. 35 m
2. 73.2 m
3. 50 m
4. 75 m
Choice B
73.2 m
CAT Geometry: Trigonometry - Trigonometric Identities

If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:
1. √2 Cos x
2. √2 Cosec x
3. √2 Sec x
4. √2 Sin x Cos x
Choice A
√2 Cos x
CAT Geometry: Circles

If \\frac {2Sinx}{1+cosx+Sinx}\\)=t, \\frac{1–Cosx+Sinx}{1+Sinx}\\) can be written as:
1. \\frac{1}{t}\\)
2. t
3. √t Sec x
4. \\frac{t}{Sinx}\\)
Choice B
4√3
CAT Geometry: Trigonometry -Height of a tree

A tall tree AB and a building CD are standing opposite to each other. A portion of the tree breaks off and falls on top of the building making an angle of 30°. After a while it falls again to the ground in front of the building, 4 m away from foot of the building, making an angle of 45°. The height of the building is 6 m. Find the total height of the tree in meters before it broke.
1. 27√3 + 39
2. 12√3 + 10
3. 15√3 + 21
4. Insufficient Data
Choice C
15√3 + 21
CAT Geometry: Trigonometry - Height of a flag pole

A flag is hoisted on top of a building of height 7√3 m. A man of height √3 m, standing on the ground, sees the top and bottom of the flag pole at 2 different angles of elevation that are found to be complementary. If the man is standing √135 m away from the building, find the height of the flag pole.
1. 3√3 m
2. 1.5√3 m
3. \\frac{2}{√3}\\) m
4. \\frac{6}{√3}\\) m
Choice B
1.5√3 m

The Questions that follow, are from actual CAT papers. If you wish to take them separately or plan to solve actual CAT papers at a later point in time, It would be a good idea to stop here.

CAT 2019 Question Paper Slot 1 - Trigonometry
The number of the real roots of the equation 2cos(x(x + 1)) = 2^x + 2^-x is
1. 0
2. Infinite
3. 1
4. 2
Choice C
1

The Questions that follow, are from actual XAT papers. If you wish to take them separately or plan to solve actual XAT papers at a later point in time, It would be a good idea to stop here.

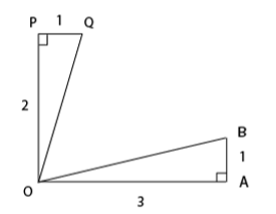
XAT 2019 Question Paper - QADI
In the trapezium ABCD the sides AB and CD are parallel. The value of \\frac{\sin \angle \mathrm{BAC}}{\sin \angle \mathrm{BAD}}) is
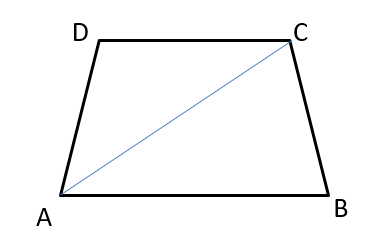
1. \\frac{\overline{A B}}{\overline{C D}})
2. \\frac{\overline{A C}}{\overline{A D}})
3. \\frac{\overline{B C}}{\overline{A D}})
4. \\frac{\overline{A D}}{\overline{A C}})
5. \\frac{\overline{A C}}{\overline{C D}})
Choice D
\\frac{\overline{A D}}{\overline{A C}})
XAT 2018 Question Paper - QADI
A boat, stationed at the North of a lighthouse, is making an angle of 30° with the top of the lighthouse. Simultaneously, another boat, stationed at the East of the same lighthouse, is making an angleof 45° with the top of the lighthouse. What will be the shortest distance between these two boats? The height of the lighthouse is 300 feet. Assume both the boats are of negligible dimensions.
1. 300 feet
2. 600/√3 feet
3. 300√3 feet
4. 600 feet
5. None of the above
Choice D
600 feet

The Questions that follow, are from actual IPMAT papers. If you wish to take them separately or plan to solve actual IPMAT papers at a later point in time, It would be a good idea to stop here.

IPMAT 2020 Sample Paper - IPM Rohtak Quants
sin\\frac{13π}{6}\\) = ?
1. \\frac{1}{2}\\)
2. \\frac{1}{\sqrt{2}}\\)
3. \\frac{1}{\sqrt{3}}\\)
4. \\sqrt{3}\\)
Choice A
\\frac{1}{2}\\)
IPMAT 2020 Question Paper - IPM Indore Quants
The value of cos²\\frac{π}{8}) + cos²\\frac{3π}{8}) + cos²\\frac{5π}{8}) + cos²\\frac{7π}{8}) is
1. 1
2. \\frac{3}{2})
3. 2
4. \\frac{9}{4})
Choice C
2
IPMAT 2019 Question Paper - IPM Indore Quants
The number of pairs (x, y) satisfying the equation sinx + siny = sin(x + y) and |x| + |y| = 1 is
6
IPMAT 2019 Question Paper - IPM Indore Quants
Given that cos x + cos y = 1, the range of sin x - sin y is
1. [-1, 1]
2. [-2, 2]
3. [0, √3]
4. [-√3, √3]
Choice D
[-√3, √3]
IPMAT 2019 Question Paper - IPM Indore Quants
If \\sin \theta + \cos \theta = m,\\) then \\sin ^{6} \theta + \cos ^{6} \theta\\) equals
1. \\frac{3(m^{2}+1)}{4}\\)
2. \\frac{3(m^{2}-1)}{4}\\)
3. \1-\frac{3(m^{2}-1)}{4}\\)
4. \1-\frac{3(m^{2}-1)^{2}}{4}\\)
Choice D
\1-\frac{3(m^{2}-1)^{2}}{4}\\)