🎉Ace the Final Stretch with our Last Mile Excellence – Your Ultimate CAT 2024 Boost!

CAT Questions | CAT Geometry Questions

CAT Quantitative Aptitude | CAT Geometry Mensuration

Mensuration is a fairly intuitive topic in CAT Geometry. Other than knowing basic formulae, structural and spatial understanding of the shapes helps one nail Mensuration questions in CAT exam. Mensuration comprises of 2D and 3D shapes including (but not limited to) Spheres, Cubes, Cuboids, Cylinders, Cones and more. You can expect at least one question from Mensuration in CAT exam. Make use of 2IIMs Free CAT Questions, provided with detailed solutions and Video explanations to obtain a wonderful CAT score. If you would like to take these questions as a Quiz, head on here to take these questions in a test format, absolutely free.

CAT Geometry: Mensuration - Data sufficiency

A right circular cone has height H and radius R. A small cone is cut off at the top by a plane parallel to the base. At what height above the base the section has been made?
Statement (I): H = 20 cm
Statement (II): Volume of small cone: volume of large cone : 1:15
1. If the question can be answered with statement I alone but not statement II alone, or can be answered with statement II alone but not statement I alone.
2. If the question cannot be answered with statement I alone or with statement II alone, but can be answered if both statements are used together.
3. If the question can be answered with either statement alone.
4. If the question cannot be answered with the information provided.
Choice B
Can be answered only if both statements are used together.
CAT Geometry: Mensuration - Sphere

A sphere of radius r is cut by a plane at a distance of h from its center, thereby breaking this sphere into two different pieces. The cumulative surface area of these two pieces is 25% more than that of the sphere. Find h.
1. r/√2
2. r/√3
3. r/√5
4. r/√6
Choice A
r/√2
CAT Geometry: Mensuration - Chords

Two mutually perpendicular chords AB and CD meet at a point P inside the circle such that AP = 6 cms, PB = 4 units and DP = 3 units. What is the area of the circle?
1. 125π/4 sq cms
2. 100π/7 sq cms
3. 125π/8 sq cms
4. 52π/3 sq cms
Choice A
125π/4 sq cms
CAT Geometry: Mensuration - Cylinders

Cylindrical cans of cricket balls are to be packed in a box. Each can has a radius of 7 cm and height of 30 cm. Dimension of the box is l = 76 cm, b = 46 cm, h = 45 cm. What is the maximum number of cans that can fit in the box?
1. 15
2. 17
3. 22
4. 21
Choice D
21
CAT Geometry: Mensuration - Triangles

PQRS is a square of sides 2 cm & ST = 2 cm. Also, PT=RT. What is the area of ∆PST?
1. 2 cm²
2. √3 cm²
3. √2 cm²
4. 1/√2 cm²
Choice C
√2 cm²
CAT Geometry: Mensuration - Length of string

A string is wound around two circular disk as shown. If the radius of the two disk are 40 cm and 30 cm respectively. What is the total length of the string?
1. 70 cm
2. 70 + 165*π cm
3. 70 + 120π cm
4. 70 + 165*π/2 cm
Choice D
70 + 165*π/2 cm
CAT Geometry: Mensuration - Cuboid

Figure above shows a box which has to be completely wrapped with paper. However, a single Sheet of paper need to be used without any tearing. The dimension of the required paper could be
1. 17 cm by 4 cm
2. 12 cm by 6 cm
3. 15 cm by 4 cm
4. 13 cm by 4 cm
Choice B
12 cm by 6 cm
CAT Geometry: Mensuration - Right Circular Cone

An inverted right circular cone has a radius of 9 cm. This cone is partly filled with oil which is dipping from a hole in the tip at a rate of 1cm3/hour. Currently the level of oil 3 cm from top and surface area is 36π cm2. How long will it take the cone to be completely empty?
1. 72π hours
2. 1 hour
3. 3 hours
4. 36π hours
Choice A
216π hours
CAT Geometry: Mensuration - Square and Triangle

A square PQRS has an equilateral triangle PTU inscribed as shown:

What is the ratio of A∆PQT to A∆TRU?
1. 1 : 3
2. 1 : √3
3. 1 : √2
4. 1 : 2
Choice D
1 : 2
CAT Geometry: Mensuration - Spheres and Cubes

A spherical shaped sweet is placed inside a cube of side 5 cm such that the sweet just fits the cube. A fly is sitting on one of the vertices of the cube. What is the shortest distance the fly must travel to reach the sweet?
1. 2.5 cm
2. 5(√3 – 1) cm
3. 5(√2 – 1) cm
4. 2.5(√3 – 1) cm
Choice D
2.5(√3 – 1) cm
CAT Geometry: Mensuration - Square shape backyard

Anil grows tomatoes in his backyard which is in the shape of a square. Each tomato takes 1 cm2 in his backyard. This year, he has been able to grow 131 more tomatoes than last year. The shape of the backyard remained a square. How many tomatoes did Anil produce this year?
1. 4225
2. 4096
3. 4356
4. Insufficient Data
Choice C
4356
CAT Geometry: Mensuration - Circles

PQRS is a circle and circles are drawn with PO, QO, RO and SO as diameters areas A and B are shaded A/B is equal to
1. π
2. 1
3. π/4
4. 2
Choice B
1
CAT Geometry: Mensuration - Square

ABCD is a square drawn inside a square PQRS of sides 4 cm by joining midpoints of the sides PQ, QR, RS, SP. Another square is drawn inside ABCD similarly. This process is repeated infinite number of times. Find the sum of all the squares.
1. 16 cm²
2. 28 cm²
3. 32 cm²
4. Infinite
Choice C
32 cm²
CAT Geometry: Mensuration - Pentagon and Circles

PQRST is a pentagon in which all the interior angles are unequal. A circle of radius ‘r’ is inscribed in each of the vertices. Find the area of portion of circles falling inside the pentagon.
1. πr²
2. 1.5πr²
3. 2πr²
4. 1.25πr²
Choice B
1.5πr²
CAT Geometry: Mensuration - Circles

Three circles with radius 2 cm touch each other as shown :-

Find the area of the circle, circumscribing the above figure.
1. 3π(4+√3)²
2. π/2(4+2√3)²
3. π/4(4+2√3)2²
4. 12π−π/2(4+2√3)²
Choice C
π/4(4+2√3)2²
CAT Geometry: Mensuration - Concentric Circles

There are 5 concentric circles that are spaced equally from each other by 1.25 cms. The innermost circle has a square of side √(32) cm inscribed in it. If a square needs to be inscribed in the outermost circle, what will be its area?
1. 324 sq. cm.
2. (66 + 40√2) sq. cm
3. 210.125 sq. cm.
4. 162 sq.cm.
Choice D
162 sq.cm.
CAT Geometry: Mensuration - Cross section of sphere

A spherical rubber ball of radius 14 cm is cut by a knife at a distance of “x” cm from its centre, into 2 different pieces. What should be the value of “x” such that the cumulative surface area of the newly formed pieces is 3/28 more than the rubber ball’s original surface area?
1. 11.4 cm
2. 3 cm
3. 12.4 cm
4. 7.5 cm
Choice C
12.4 cm

The Questions that follow, are from actual CAT papers. If you wish to take them separately or plan to solve actual CAT papers at a later point in time, It would be a good idea to stop here.

CAT 2023 Slot 3 - QA

A rectangle with the largest possible area is drawn inside a semicircle of radius \(2 \mathrm{~cm}\). Then, the ratio of the lengths of the largest to the smallest side of this rectangle is
1. \(2 : 1\)
2. \(\sqrt{5} : 1\)
3. \(1 : 1\)
4. \(\sqrt{2} : 1\)
Choice A
\(2 : 1\)
CAT 2022 Slot 1 - QA

A trapezium \(\text{ABCD}\) has side \(\text{AD}\) parallel to \(\text{BC}, \angle \text{BAD}=90^{\circ}, \text{BC}=3 \text{~cm}\) and \(\text{AD}=8 \text{~cm}\). If the perimeter of this trapezium is \(36 \text{~cm}\), then its area, in sq. \(\text{cm}\), is
66
CAT 2022 Slot 1 - QA

All the vertices of a rectangle lie on a circle of radius \(R\). If the perimeter of the rectangle is \(P\), then the area of the rectangle is
1. \(\frac{P^2}{2}-2 P R\)
2. \(\frac{P^2}{8}-2 R^2\)
3. \(\frac{P^2}{16}-R^2\)
4. \(\frac{P^2}{8}-\frac{R^2}{2}\)
Choice B
\(\frac{P^2}{8}-2 R^2\)
CAT 2021 Slot 3 - QA

Let ABCD be a parallelogram. The lengths of the side AD and the diagonal AC are 10 cm and 20 cm, respectively. If the angle ∠ADC is equal to 30° then the area of the parallelogram, in sq. cm, is
1. \(\frac{25(\sqrt{3}+\sqrt{15})}{2}\)
2. \(25(\sqrt{5}+\sqrt{15})\)
3. \(\frac{25(\sqrt{5}+\sqrt{15})}{2}\)
4. \(25(\sqrt{3}+\sqrt{15})\)
Choice D
\(25(\sqrt{3}+\sqrt{15})\)

Correct: 9.46%
Incorrect: 10.87%
Unattempted: 79.67%
CAT 2021 Slot 3 - QA

A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is
3500

Correct: 21.12%
Incorrect: 26.38%
Unattempted: 52.5%
CAT 2021 Slot 3 - QA

The cost of fencing a rectangular plot is ₹ 200 per ft along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is
1. 90000
2. 160000
3. 120000
4. 100000
Choice C
120000

Correct: 30.55%
Incorrect: 10.8%
Unattempted: 58.65%
CAT 2021 Slot 2 - QA

The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is
1. 20
2. 25
3. 40
4. 30
Choice D
30

Correct: 34.97%
Incorrect: 9.07%
Unattempted: 55.96%
CAT 2020 Question Paper Slot 2 - Mensuration

The sum of perimeters of an equilateral triangle and a rectanmgle is 90 cm. The area, T, of the triangle and the area , R, of the rectangle, both in sq cm, satisfy the relationship R = T². If the sides of the rectangle are in the ratio 1 : 3, then the length, in cm, of the longer side of the rectangle, is
1. 27
2. 18
3. 21
4. 24
CAT 2020 Question Paper Slot 1 - Mensuration

A solid right circular cone of height 27 cm is cut into 2 pieces along a plane parallel to it's base at a height of 18 cm from the base. If the difference in the volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
1. 264
2. 232
3. 243
4. 256
CAT 2020 Question Paper Slot 1 - Mensuration

On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches opposite two sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
1. 3√π(5 + \\frac{12}{π}))
2. 4√π(3 + \\frac{12}{π}))
3. 5√π(3 + \\frac{12}{π}))
4. 3√π(\\frac{5}{2}) + \\frac{6}{π}))
CAT 2019 Question Paper Slot 2 - Mensuration

The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is
1. 10\\sqrt{2})
2. 8\\sqrt{3})
3. 12
4. 5\\sqrt{5})
Choice A
10\\sqrt{2})
CAT 2019 Question Paper Slot 2 - Mensuration

A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is
1. 1044(4 + π)
2. 8464π
3. 928π
4. 1026(1 + π)
Choice D
1026(1 + π)
CAT 2019 Question Paper Slot 1 - Mensuration

Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is
1. 5 : 6
2. 3 : 4
3. 2 : 3
4. 4 : 5
Choice C
2 : 3
CAT 2019 Question Paper Slot 1 - Mensuration

If the rectangular faces of a brick have their diagonals in the ratio 3 : 2 \\sqrt{3}) : \\sqrt{15}), then the ratio of the length of the shortest edge of the brick to that of its longest edge is
1. 1 : \\sqrt{3})
2. 2 : \\sqrt{5})
3. \\sqrt{2}) :\\sqrt{3})
4. \\sqrt{3}) : 2
Choice A
1 : \\sqrt{3})
CAT 2018 Question Paper Slot 2 - Mensuration

From a rectangle ABCD of area 768 sq cm, a semicircular part with diameter AB and area 72π sq cm is removed. The perimeter of the leftover portion, in cm, is
1. 88 + 12π
2. 80 + 16π
3. 86 + 8π
4. 82 + 24π
Choice A
88 + 12π
CAT 2018 Question Paper Slot 2 - Mensuration

The area of a rectangle and the square of its perimeter are in the ratio 1 : 25. Then the lengths of the shorter and longer sides of the rectangle are in the ratio
1. 3 : 8
2. 2 : 9
3. 1 : 4
4. 1 : 3
Choice C
1 : 4
CAT 2018 Question Paper Slot 2 - Mensuration

A parallelogram ABCD has area 48 sqcm. If the length of CD is 8 cm and that of AD is s cm, then which one of the following is necessarily true?
1. s ≥ 6
2. s ≠ 6
3. 5 ≤ s ≤ 7
4. s ≤ 6
Choice A
s ≥ 6
CAT 2018 Question Paper Slot 1 - Mensuration

A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is:[TITA]
198
CAT 2018 Question Paper Slot 1 - Mensuration

In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is
1. 18√3
2. 24√3
3. 32√3
4. 12√3
Choice C
32√3
CAT 2017 Question Paper Slot 1 - Mensuration & Geometry

A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8: 27: 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to:
1. 10
2. 50
3. 60
4. 20
Choice B
50
CAT 2017 Question Paper Slot 1 - Mensuration & Geometry

A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is 9 π cm³. Then the vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is: (TITA)
6

The Questions that follow, are from actual XAT papers. If you wish to take them separately or plan to solve actual XAT papers at a later point in time, It would be a good idea to stop here.

XAT 2020 Question Paper - QADI
A man is laying stones, from start to end, along the two sides of a 200-meter-walkway.The stones are to be laid 5 meters apart from each other. When he begins, all the stones are present at the start of the walkway. He places the first stone on each side at the walkway’s start. For all the other stones, the man lays the stones first along one of the walkway’s sides, then along the other side in an exactly similar fashion. However, he can carry only one stone at a time. To lay each stone, the man walks to the spot, lays the stone, and then walks back to pick another. After laying all the stones, the man walks back to the start, which marks the end of his work. What is the total distance that the man walks in executing this work? Assume that the width of the walkway is negligible.
1. 16200 meters
2. 8200 meters
3. 8050 meters
4. 16400 meters
5. 4100 meters
Choice D
16400 meters
XAT 2020 Question Paper - QADI
A rectangular swimming pool is 50 meters long and 25 meters wide. Its depth isalways the same along its width but linearly increases along its length from 1 meter atone end to 4 meters at the other end. How much water (in cubic meters) is needed tocompletely fill the pool?
1. 3750
2. 2500
3. 1250
4. 1874
5. 3125
Choice E
3125
XAT 2020 Question Paper - QADI
Six drums are used to store water. Five drums are of equal capacity, while the sixth drum has double the capacity of each of these five drums. On one morning, three drums are found half full, two are found two-thirds full and one is found completely full. It is attempted to transfer all the water to the smaller drums. How many smaller drums are adequate to store the water?
1. Four but not three
2. Three or four, depending on which drum had how much water initially
3. Five but not four
4. Five may be inadequate, depending on which drum had how much water initially
5. Three but not two
Choice C
Five but not four
XAT 2020 Question Paper - QADI
In the figure given below, the circle has a chord AB of length 12 cm, which makes an angle of 60 at the center of the circle, O. ABCD, as shown in the diagram, is a rectangle. OQ is the perpendicular bisector of AB, intersecting the chord AB at P, the arc AB at M and CD at Q. OM = MQ. The area of the region enclosed by the line segments AQ and QB, and the arc BMA, is closest to (in cm²):
1. 137
2. 63
3. 35
4. 69
5. 215
Choice D
69
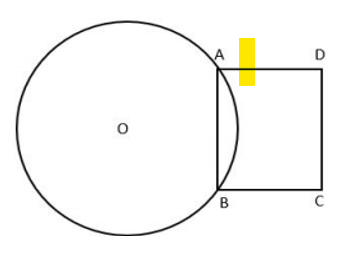
XAT 2020 Question Paper - QADI
Mohanlal, a prosperous farmer, has a square land of side 2 km. For the current season, he decides to have some fun. He marks two distinct points on one of the diagonals of the land. Using these points as centers, he constructs two circles. Each of these circles falls completely within the land, and touches at least two sides of the land. To his surprise, the radii of both the circles are exactly equal to 2/3 km. Mohanlal plants potatoes on the overlapping portion of these circles.
Calculate the area on which Mohanlal planted potatoes (in sq. km).
1. 5( 𝜋 + 4)/27
2. 2(2 𝜋 − 3 √3 )/27
3. 4(𝜋 − 3 √3 )/27
4. 𝟐(𝝅 − 2)/9
5. (𝝅 − 2)/9
Choice D
𝟐(𝝅 − 2)/9
XAT 2019 Question Paper - QADI
A gold ingot in the shape of a cylinder is melted and the resulting molten metal molded into a few identical conical ingots. If the height of each cone is half the height of the original cylinder and the area of the circular base of each cone is one ﬁfth that of the circular base of the cylinder, then how many conical ingots can be made?
1. 60
2. 10
3. 30
4. 20
5. 40
Choice C
30
XAT 2018 Question Paper - QADI
It takes 2 liters to paint the surface of a solid sphere. If this solid sphere is sliced into 4 identical pieces, how many liters will be required to paint all the surfaces of these 4 pieces.
1. 2.2 liters
2. 2.5 liters
3. 3.0 liters
4. 4.0 liters
5. None of the above
Choice D
4.0 liters
XAT 2018 Question Paper - QADI
A cone of radius 4 cm with a slant height of 12 cm was sliced horizontally, resulting into a smaller cone (upper portion) and a frustum (lower portion). If the ratio of the curved surface area of the upper smaller cone and the lower frustum is 1:2, what will be the slant height of the frustum?
1. 12 – √3
2. 12 – 2√3
3. 12 – 3√3
4. 12 – 4√3
5. None of the above
Choice D
12 – 4√3

The Questions that follow, are from actual IPMAT papers. If you wish to take them separately or plan to solve actual IPMAT papers at a later point in time, It would be a good idea to stop here.

IPMAT 2020 Sample Paper - IPM Rohtak Quants
Use the figure below to answer the folowing questions.

What is the area of the shaded figure?
1. 56.25π square feet
2. 112.5π square feet
3. 225π square feet
4. 337.4π square feet
Choice B
112.5 \\pi\\)
IPMAT 2020 Sample Paper - IPM Rohtak Quants
What is the ratio of the area of Circle M and the area of Circle K?
1. 1 : 8
2. 1 : 4
3. 1 : 2
4. 1 : 1
Choice B
1:4
IPMAT 2020 Sample Paper - IPM Rohtak Quants
A room has floor size of 15*6sq.cm. What is the height of the room , if the sum of the areas of the base and roof is equal to the sum of the areas of the four walls ?
1. 1.12cm
2. 3.24cm
3. 4.29cm
4. 2.5cm
Choice A
1.12cm
IPMAT 2020 Sample Paper - IPM Rohtak Quants
What decimal of an hour is a second?
1. .00028
2. .00027
3. .00026
4. .00025
Choice B
.0027
IPMAT 2020 Sample Paper - IPM Rohtak Quants
What will be vulgar fraction of 0.0056?
1. \\frac{7}{1150}\\)
2. \\frac{7}{1175}\\)
3. \\frac{7}{1250}\\)
4. \\frac{7}{1275}\\)
Choice C
\\frac{7}{1250}\\)
IPMAT 2020 Sample Paper - IPM Rohtak Quants
A circle is inscribed in an equilateral triangle of side 24 cm, touching its sides. What is the area of
the remaining portion of the triangle?
1. 144√3 - 48π cm²
2. 121√3 - 36π cm²
3. 144√3 - 36π cm²
4. 121√3 - 48π cm²
Choice A
144√3 - 48π cm²
IPMAT 2020 Sample Paper - IPM Rohtak Quants
A clock strikes 4 taking 9 seconds. In order to strike 12 at the same rate, the time taken is
1. 33 seconds
2. 30 seconds
3. 36 seconds
4. 27 seconds
Choice A
33 seconds
IPMAT 2019 Question Paper - IPM Indore Quants
The number of whole metallic tiles that can be produced by melting and recasting a circular metallic plate, if each of the tiles has a shape of a right-angled isosceles triangle and the circular plate has a radius equal in length to the longest side of the tile (Assume that the tiles and plate are of uniform thickness, and there is no loss of material in the melting and recasting process) is
12
IPMAT 2019 Question Paper - IPM Indore Quants
Three cubes with integer edge lengths are given. It is known that the sum of their surface areas is 564 cm² Then the possible values of the sum of their volumes are
1. 764 cm³ and 586 cm³
2. 586 cm³and 564 cm³
3. 764 cm³ and 564 cm³
4. 586 cm³ and 786 cm³
Choice A
764 cm³ and 586 cm³