CAT Quantitative Aptitude Questions | CAT Ratios, Mixtures, Alligations and Averages Questions

The question is from CAT Ratio, Mixtures and Averages. Three mixtures with different capcity are mixed together. What would be the ratio in the resultant solution? CAT exam is known to test on basics rather than high funda ideas. A range of CAT questions can be asked from Ratios and Proportions, Mixtures, Alligations and Averages. Make sure you master the topics. 2IIMs CAT questions bank provides you with CAT questions that can help you gear for CAT Exam CAT 2023.

Question 37: What would be the ratio of milk and water in a final mixture formed by mixing milk and water that are present in three vessels of capacity 1l, 2l, and 3l respectively and in the ratios 5:1, 3:2 and 4:3 respectively?

1. 747:443
2. 787:1260
3. 787:473
4. 747:473

Explanatory Answer

Method of solving this CAT Question from Ratio, Mixtures and Averages: When we mix two mixtures in a particular ratio, we get a third mixture. Given the third mixture how does one find the ratio in which they were mixed.

Solve this type of questions by taking 2 at a time. Take the first 2 vessels,
In 1st, fraction of milk = \\frac{5}{6}\\)
In 2nd, fraction of milk = \\frac{3}{5}\\)
Therefore,

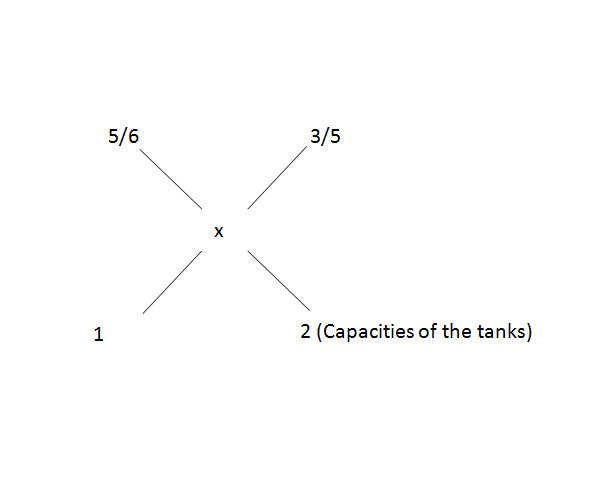
=> \\frac{3/5 - x}{x - 5/6}\\) = \\frac{1}{2}\\)
=> \\frac{6}{5}\\) - 2x = x - \\frac{5}{6}\\)
=> \\frac{6}{5}\\) + \\frac{5}{6}\\) = 3x
=> x = \\frac{61}{90}\\) (And the volume of mixture after mixing = 1 + 2 = 3 l)
Therefore,

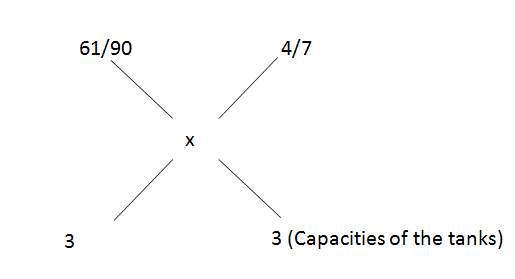
=> \\frac{4/7 - x}{x - 61/90}\\) = \\frac{3}{3}\\)
=> \\frac{4}{7}\\) - x = x + \\frac{61}{90}\\)
=> \\frac{4}{7}\\) + \\frac{61}{90}\\) = 2x
=> 2x = \\frac{787}{630}\\) => x = \\frac{787}{1260}\\)
Therefore, Milk : Water = \\frac{787}{(1260 - 787)}\\) = \\frac{787}{473}\\)

The question is "What would be the ratio of milk and water in a final mixture formed by mixing milk and water that are present in three vessels of capacity 1l, 2l, and 3l respectively and in the ratios 5:1, 3:2 and 4:3 respectively?"

Hence, the answer is "787:473".

Choice C is the correct answer.