CAT Questions | CAT LR DI

CAT DI LR section has become increasingly tough beginning from 2015. However, Understanding the basics of Bar graphs, Pie Charts, Multiple graphs, Line Graphs etc forms an integral part of solving tougher CAT level DI LR questions for the CAT Exam. This question is from Logical Reasoning for CAT - Math Puzzles.

Logical Reasoning for CAT: Math Puzzles

Xuomi's Hotel

Xuomi wants to convert his two storey house that has 5 rooms each in two floors into a hotel. Xuomi decides to number his first floor rooms with 5 consecutive numbers in the 100's, and his second floor numbers would be 5 consecutive numbers in the 200's. Goes without saying that the 5 room numbers in the 2nd floor are 100 more than the corresponding room numbers from the first floor.

Being a mathematician, Xuomi is extremely fascinated by primes and also unconcerned about other people's preference for simple sequences. So, he decides to number his rooms in such a way as to have as many prime numbers as possible. His friend, Pytha told him blithely that the maximum he could manage was 5 numbers. Xuomi generated the maximum amount of contempt possible with his eyes and told his friend that not even his father (Pytha's father, not Xuomi's) Goras could accommodate 5 primes and 4 primes was the limit of anyone's ambition.

So, they decided to go for 4. Pytha suggested that they might want to go for numbers such that average number of all the room numbers put together would also be prime. Xuomi checked his math and told him this was possible.

Xuomi also wanted the first room, or the room with the least number to be prime and then went on to number his rooms accordingly.

Needless to say, the hotel was a phenomenal project. The mathematicians who visited the project were mighty impressed and recommended it to all their friends. With mathematicians from all over the world making it a point to stay here at least once, demand went through the roof. Having said that, all the mathematicians wanted to stay in prime number rooms and so occupancy never crossed 40%.

Xuomi went out of business and sold his property to Mr. Frump who made millions by making it a casino.

Question 4: What is the overall average of the 10 room numbers?

Video Explanation

Explanatory Answer

Method of solving this Question on Logical Reasoning for CAT

General Solution

This is an almost impossibly tough question if you do not have a grasp on finding prime numbers. Fortunately, it will be well worth our time to find the three digit prime numbers under 300, since the whole question is based on this. Since we only have to check up to 300, we have to bother checking all multiples of primes 17 and under only (since 17 square is 289). Let's create a table where we list down all odd numbers under 300, and eliminating all multiples of 3 and 5 (these are the easiest odd numbers to eliminate since divisibility test for 3 is straightforward.)

We get this table:

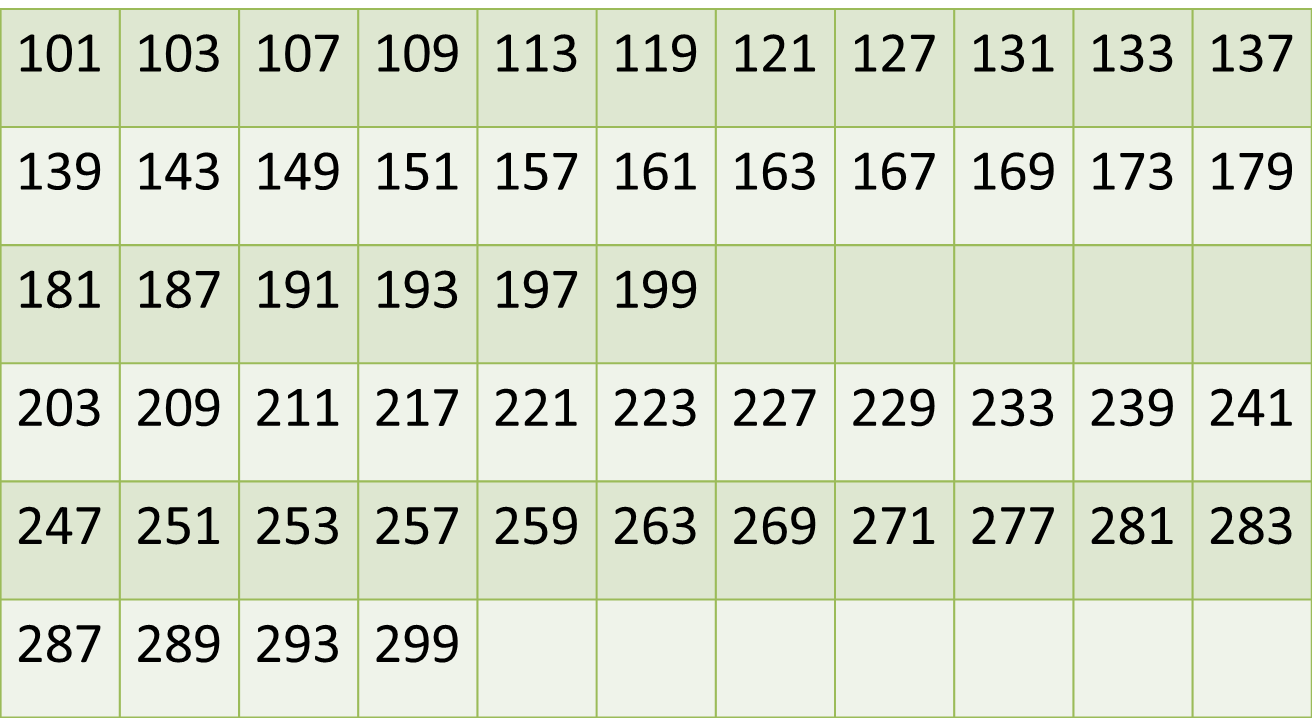
We can list all odd multiples of 7, 11, 13 and 17 above 100 and under 300 and cross this off our table.

Multiples of 7: 105, 119, 133, 147, 161, 175, 189, 203, 217, 231, 245, 259, 273, 287 (We can generate this list quickly by step counting 14).

Multiples of 11:121, 143, 165, 187, 209, 231, 253, 275, 287 (We can generate this list quickly by step counting 22).

Multiples of 13:117, 143, 169, 195, 221, 247, 273, 299 (We can generate this list by step counting 26). Multiples of 17:119, 153, 187, 221, 255, 289 (We can generate this by step counting 34).

Now, if we cross out any common numbers in our list and the table that we drew earlier, we will have a list of all prime numbers under 300. This whole process is just an application of the Sieve of Eratosthenes (more interesting stuff to read about!)

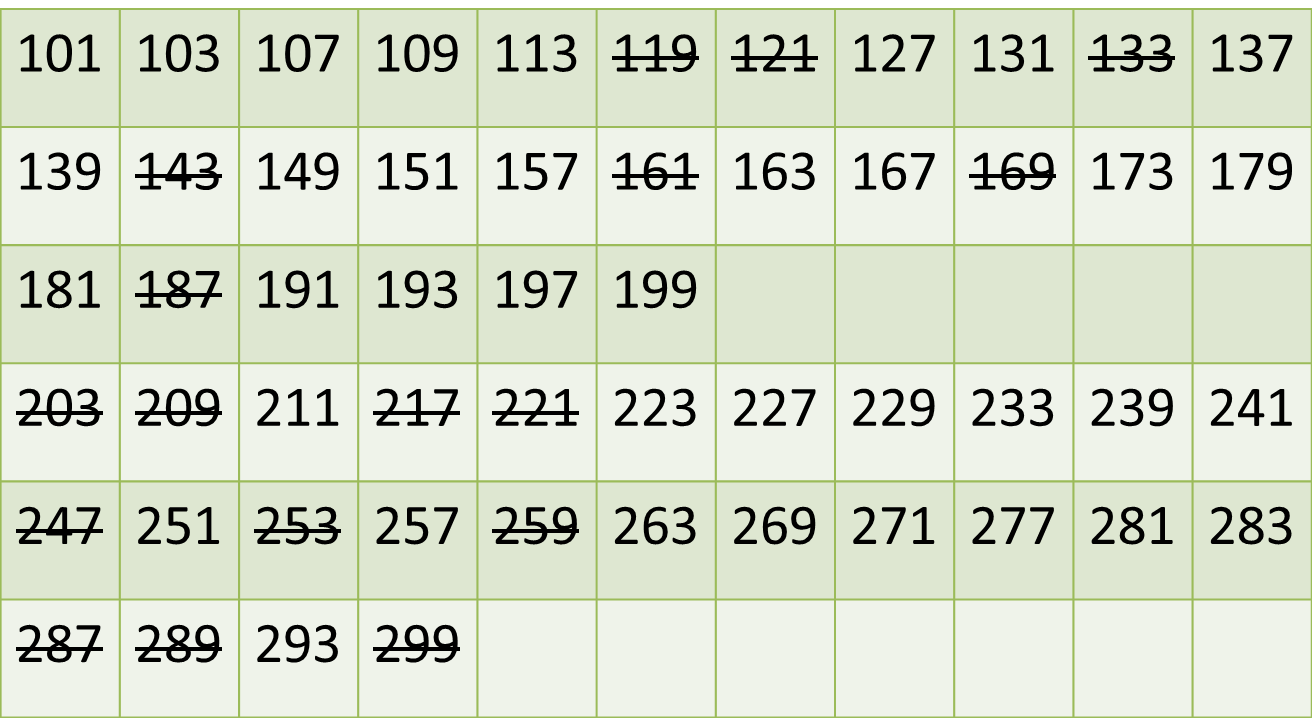
Now that we have all the primes, we've got to do a little thinking. We've got two lists of five consecutive numbers to work with. Also, the puzzle tells us this list behaves like this: If the first floor had numbers 101, 102, 103, 104, 105; the second floor has 201, 202, 203, 204, 205.

In any list of 5 consecutive numbers, we can have a maximum of three odd numbers. Our required prime numbers will definitely be odd. Also, no three consecutive odd numbers can be concurrently prime. Think about this. The numbers can be of the form 'n', 'n+2', and 'n+4'. One of these three odd numbers will definitely be a multiple of 3 (try to prove this, it's quite fun to establish).

This essentially means that one floor cannot have 3 primes. This in turn implies that each floor should have exactly 2 primes. So any set of two primes that are within the range of 5 consecutive numbers needs to be looked at. This also means that one pair of primes (at least) will be have common ten's and unit's digits (that is 1ab and 2ab. Let's refine our table a little bit to show only the primes:

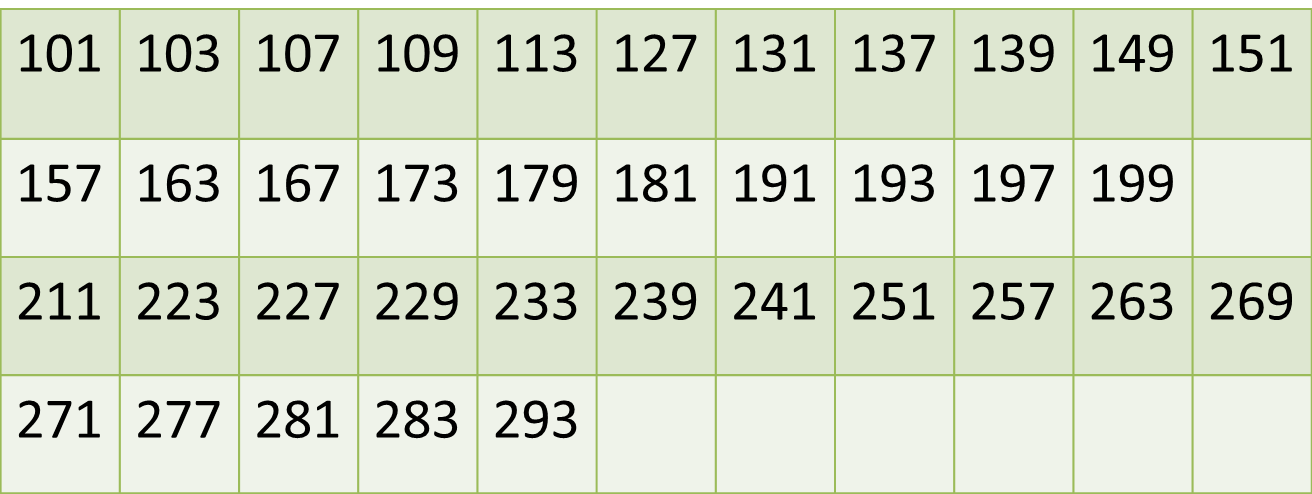
Let's look at the primes in the 200 series (There are fewer to work with). From this point it is trial and error. We notice that 227 and 229 are a possible pair, and so are 127 and 131. A possible sequence of numbers can be 127, 128, 129, 120, 131, and 227, 228, 229, 230 and 231.

Another possible pair is 239 and 241. We notice that 137 and 139 are also close together. So another sequence is 137, 138, 139, 140, 141, and 237, 238, 239, 240, 241.

Another pair is 277 and 281. We notice that 179 and 181 are also close together. So another sequence is 177, 178, 179, 180, 181 and 277, 278, 279, 280 and 281. The final pair is 281 and 283. The sequence is 179, 180, 181, 182, 183 and 279, 280, 281, 282, 283. The possible room numbers are listed below, with the primes in red. The average of all room numbers in each sequence should also be a prime number

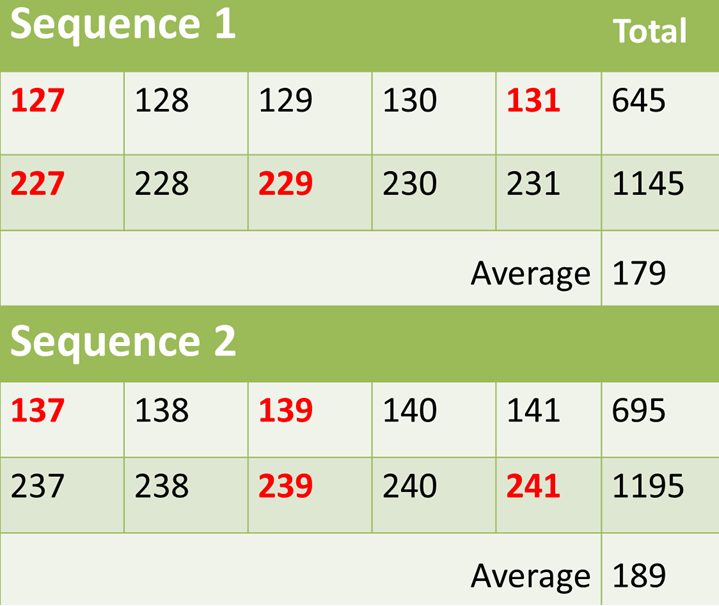
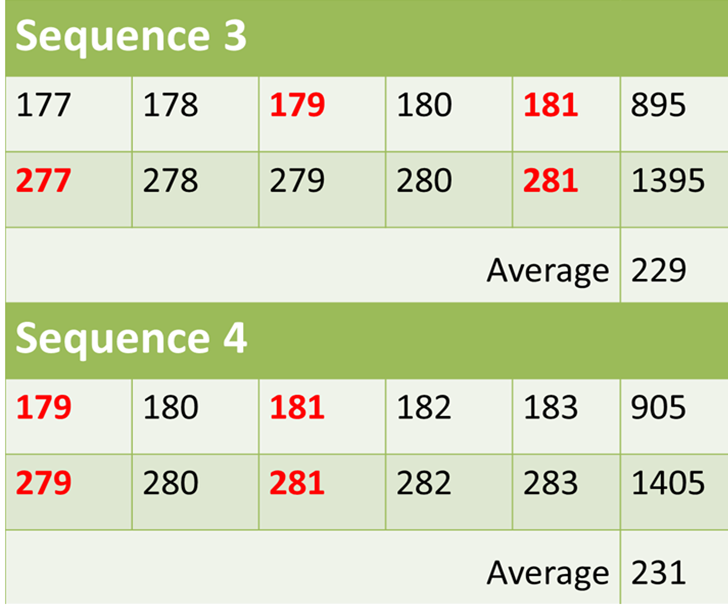
We see that there there are two possibilities. Both Sequence 1 and 3 are possible solutions at this stage. But Xuomi said he wanted the first room on the first floor to also be a prime number. This is possible only in Sequence 1. So this is the answer.

The overall average is 179 that has already been calculated. We did this to satisfy one of the conditions (refer to the table above).

The question is "What is the overall average of the 10 room numbers?"

Hence, the answer is "179".